Relationship between continuous-time and discrete-time Fourier transforms
Previously in my Fourier transforms series I've talked about the continuous-time Fourier transform and the discrete-time Fourier transform. Today it's time to start talking about the relationship between these two.
Let's start with the idea of sampling a continuous-time signal, as shown in this graph:

Mathematically, the relationship between the discrete-time signal and the continuous-time signal is given by:

(When I write equations involving both continuous-time and discrete-time quantities, I will sometimes use a subscript "c" to distinguish them.)
The sampling frequency is  (in Hz) or
(in Hz) or  (in radians per second).
(in radians per second).
The discrete-time Fourier transform of  is related to the continuous-time Fourier transform of
is related to the continuous-time Fourier transform of  as follows:
as follows:

But what does that mean? There are two key pieces to this equation. The first is a scaling relationship between  and
and  :
:  . This means that the sampling frequency in the continuous-time Fourier transform,
. This means that the sampling frequency in the continuous-time Fourier transform,  , becomes the frequency
, becomes the frequency  in the discrete-time Fourier transform. The discrete-time frequency
in the discrete-time Fourier transform. The discrete-time frequency  corresponds to half the sampling frequency, or
corresponds to half the sampling frequency, or  .
.
The second key piece of the equation is that there are an infinite number of copies of  spaced by
spaced by  .
.
Let's look at a graphical example. Suppose  looks like this:
looks like this:

Note that  equals zero for all frequencies
equals zero for all frequencies  . This is what we mean when we say a continuous-time signal is band-limited. The frequency
. This is what we mean when we say a continuous-time signal is band-limited. The frequency  is called the bandwidth of the signal.
is called the bandwidth of the signal.
The discrete-time Fourier transform of  looks like this:
looks like this:

where  . As I mentioned before, normally only one period of
. As I mentioned before, normally only one period of  is shown:
is shown:

For this example, then,  between
between  and
and  looks just like a scaled version of
looks just like a scaled version of  .
.
Next time we'll consider what happens when  doesn't look like
doesn't look like  . In other words, we're about to tackle aliasing.
. In other words, we're about to tackle aliasing.
- Category:
- Fourier transforms
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building


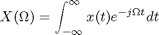




Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.