I’d like to introduce Frantz Bouchereau, development manager for Signal Processing Toolbox who is going to dive deep into insights on deep learning for signal processing, including the complete deep learning workflow for signal processing applications. It's a longer post than usual, but jam packed with actionable information. Enjoy!

Introduction
Today we will highlight signal processing applications using deep learning techniques. Deep Learning developed and evolved for image processing and computer vision applications, but it is now increasingly and successfully used on signal and time series data.
Deep learning is becoming popular in many industries including (but not limited to) the following areas:

The unifying theme in these applications is that the data is not images but signals coming from different types of sensors like microphones, electrodes, radar, RF receivers, accelerometers, and vibration sensors. The collection of large signal datasets is enabling engineers to explore new and exciting deep learning applications.
Signal Processing vs. Image Processing
Deep learning for signal data typically requires preprocessing, transformation, and feature extraction steps that image processing applications often do not. While large high-quality
image datasets can be created with relatively low-cost cameras, signal sets are harder to obtain and will usually suffer from large variability caused by wideband noise, interference, non-linear trends, jitter, phase distortion, and missing samples.
While it is likely that you will be able to successfully train a deep model with a large set of high-quality raw images fed directly into a network, you will probably not succeed doing the same with a limited size, low SNR signal data set.
Knowledge vs. Data
We don’t always have the luxury of having large signal data sets. Signals may be difficult to measure, or the application may not be easily observable. For example, consider the case of predicting remaining useful life of a machine. Fortunately, we live in a time where most machines work properly, so failure data will be less prevalent than healthy data.
Being successful with deep learning for signal processing applications depends on your dataset size, your computational power, and how much knowledge you have about the data. You can visualize this in the figure below:
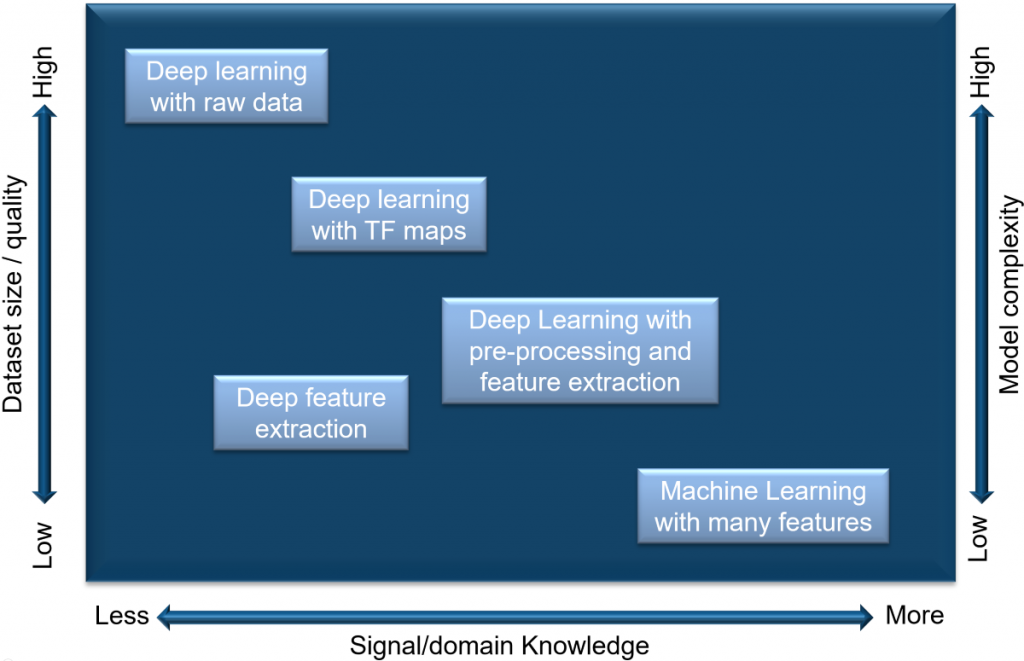
The larger and higher quality the dataset, the closer you can get to being able to perform deep learning with raw signal data. Similarly, if you have higher computational power, you will be able to train more complex networks that will improve performance.
On the other hand, if you understand your data, you may be successful extracting key features to feed into a traditional machine learning algorithm without the need of a large dataset and of a deep network. This requires more signal processing knowledge, but results can be impressive.
Between the two extremes of raw signal data and crafting a customized machine learning approach are some interesting considerations:
- A popular technique is to use time-frequency transformations to be able to use transfer learning on a pretrained convolutional neural network (CNN) similar to an image classification workflow. (See example)
- Another is to preprocess the signal and extract some features to decrease the variability by increasing the prominence of the features that matter to the application. (See example)
- Another technique is to use wavelet scattering to automatically extract a low variant set of features that are likely to enhance the performance of your learning algorithm. (See example)
Note that adding feature extraction steps also offers other advantages, such as data-dimensionality reduction that can significantly reduce training and processing times.
Another solution to having limited data sets is to augment them, or to generate synthetic signals using simulation, which we'll discuss more in the preprocessing section of the workflow.
Deep learning for signals workflow
The figure below depicts a typical end-to-end deep learning workflow for signal processing applications. Although most discussions about deep learning focus on the predictive model development, there are other equally important steps:
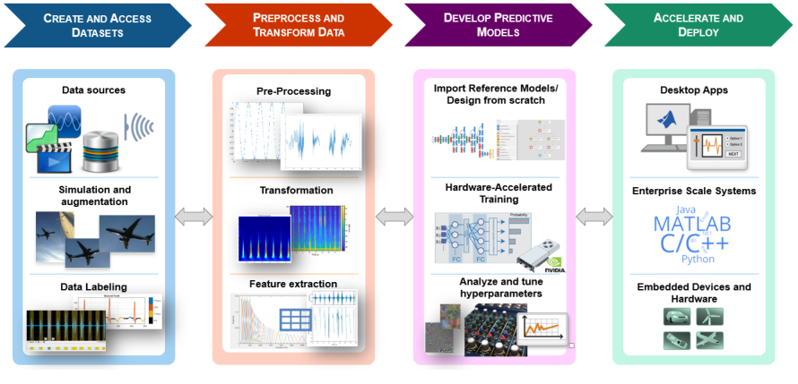
Next we’ll walk through each of these steps, addressing what to do when:
- You don't have enough data, or the exact opposite problem: You have too much data that needs to be labeled.
- Feature extraction and signal transformations require domain knowledge. In cases where domain knowledge is limited, the availability of reference architectures helps to get a head start but such architectures are quite limited in signal processing applications.
- Deploying the trained model across multiple platforms is not an easy task, at it requires C or GPU code generation.
I'll also highlight new capabilities you can use in the latest release.
Manage Data
Typically, you will need to read your signal and label data, preprocess, transform, and extract features from it, then split it into training and testing sets, and feed it into a model.
Here are specific tools to manage your signal data sets:
- Datastores: Datastores can help you read signal data from files without the risk of running out of memory. You can use the 'transform' method of a datastore to preprocess and extract features as you read the data. Datastores also split your dataset into training and tests sets. There are a few datastores to choose from depending on your file type: for example, audioDatastore, fileDatastore, and imageDatastore.
| Signal Labeling: Supervised learning problems require data sets with ground truth labels. If your data set is large, adding labels can be a lengthy process. Signal Labeler app, (new in 19a), helps to label signal attributes, regions, and points of interest. Then you can visualize and navigate through the labels in time. |
 |
- Synthetic data generation and augmentation: As you start using your dataset to train a model, you may find that you need more data to improve accuracy or increase robustness. When recording and labeling real-world data is impractical or unreasonable, creating synthetic data sets through simulation is an option.
Another common strategy consists of generating additional signals by applying variations, nuances, and transformations to the original dataset. For example, in a speech dataset consisting of spoken words, you can take one sample of a word, and alter its pitch/frequency and duration, or you can add nuances such as background noise to effectively turn one data entry into several new entries.
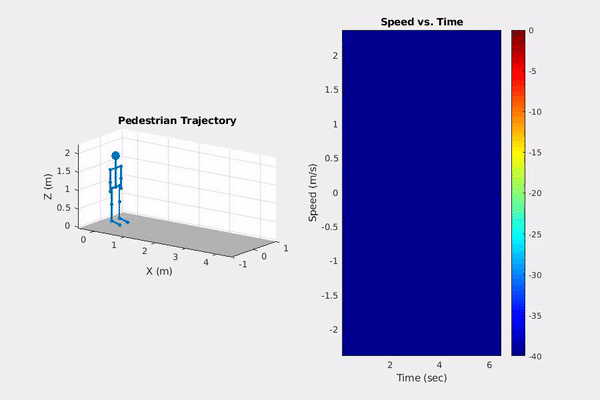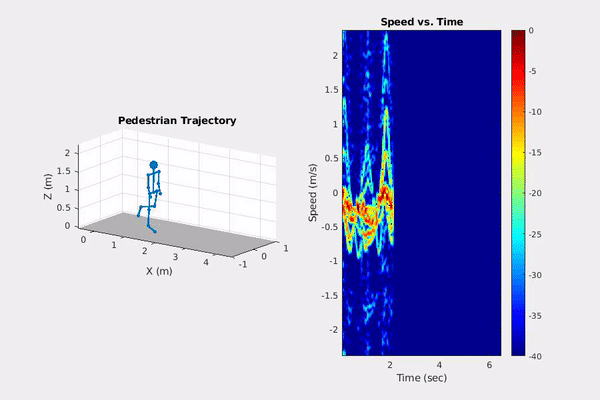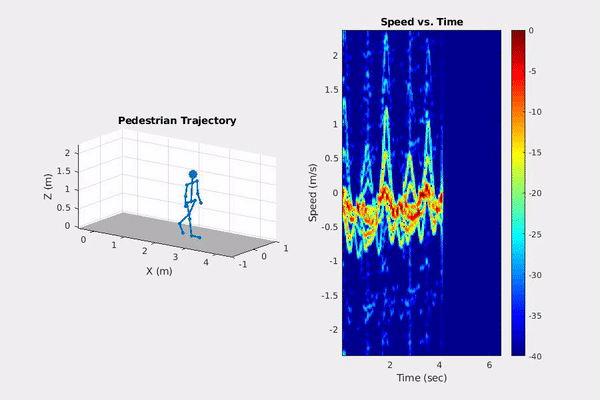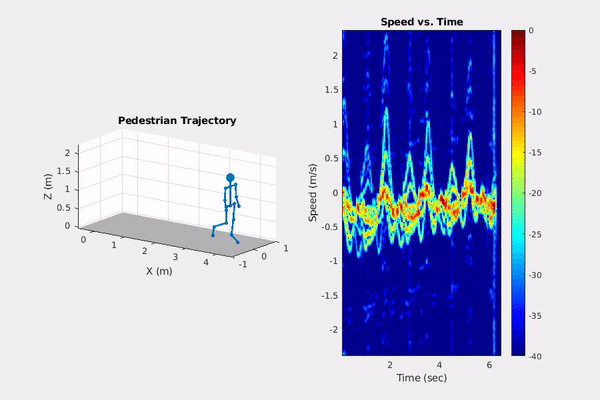 Phased Array System Toolbox offers functionality to model micro-doppler radar signatures of pedestrians (new in 19a) that can be used in automated driving applications.
Phased Array System Toolbox offers functionality to model micro-doppler radar signatures of pedestrians (new in 19a) that can be used in automated driving applications.
Visualize, Preprocess and Extract Features
When you are trying to figure out what type of preprocessing and feature extraction you need for your signals, a common first step is to visualize and explore the signals in multiple domains.
Signal Analyzer app allows you to navigate through signals in the time, frequency, and time-frequency domains, extract regions of interest, transform the data and explore preprocessing steps.
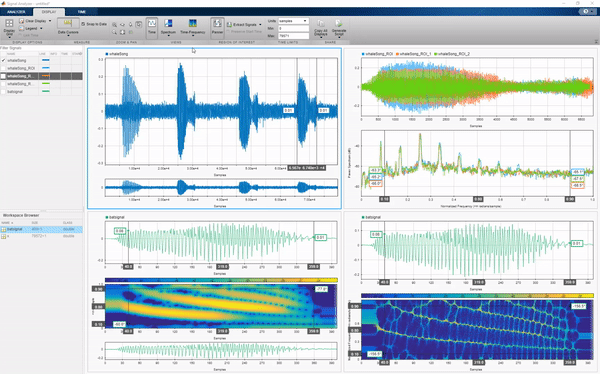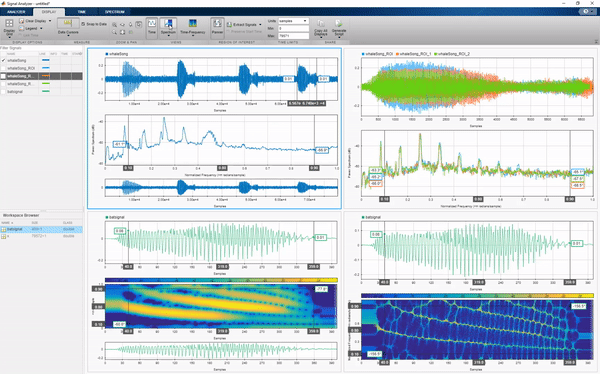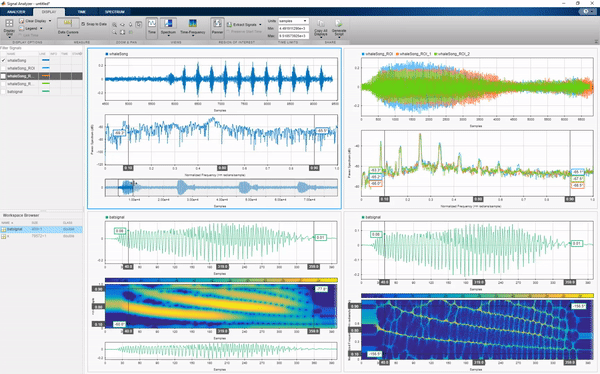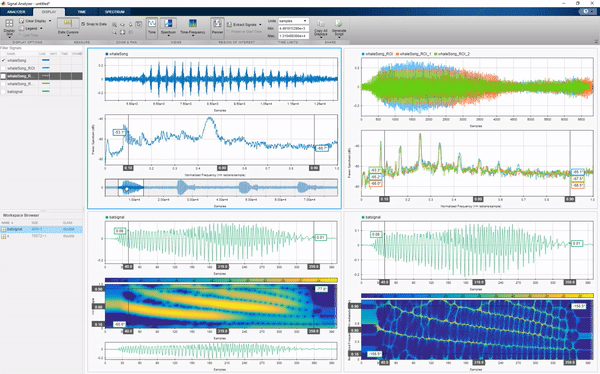
There are other apps as well, including:
- Signal Multiresolution Analyzer, which decomposes signals into time-aligned components. This allows you to pick only the signal components that matter and use these to train a model.
- Signal Denoiser, (included in Wavelet Toolbox) which helps to smooth and denoise signals.
All these apps generate MATLAB code, which you can then use to process your entire dataset after interactively determining the right approach.
Transform & Extract Features
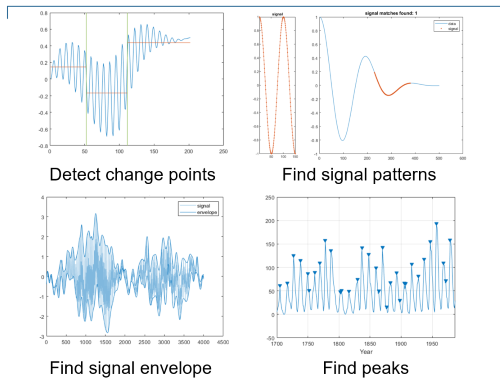
While apps make getting started easier, users familiar with Signal Processing Toolbox and Wavelet Toolbox will know we also have hundreds of command line functions to enable more advanced workflows. We have time-domain feature extraction tools to find signal patterns, detect signal envelopes and change points.
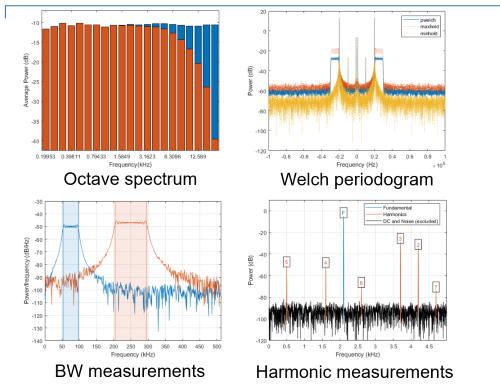
There are a variety of spectral functions to measure power, bandwidth and harmonics.
And there are time-frequency transformation functions, from continuous wavelet transform, to Wigner-Ville distribution and short-time Fourier transform, which are commonly used in deep learning applications.
You can choose the transform that best suits your time and frequency resolution needs.

There are also functions to extract features specific to audio and speech, radar, sensor fusion and text analytics applications, which we will save for a future post.
Links to signal-specific processing functionality can be found here:
Wavelet Scattering:
A wavelet scattering network (new in 18a) is a deep network with fixed weights that are set to wavelets. This feature extractor returns low variant features that can be used in conjunction with a machine or deep learning model to produce highly accurate results with few parameters to tweak.
Wavelet scattering is a great alternative for non-signal processing experts as it automatically extracts relevant features without the need to have expertise on the nature of the data.
To see wavelet scattering in action, here are some examples:
Code Generation
In 19a, there are significant advancements to automatic C code generation support for signal processing workflows, including support for filtering functions, spectral analysis, and the continuous wavelet transform (cwt). In 19a Wavelet Toolbox also added GPU code generation support for cwt. A complete list of signal processing and wavelet supported functions is here (
Signal Processing Toolbox code generation support,
Wavelet Toolbox code generation support).
List of new examples
Finally, to see a list of new examples for deep learning for signal processing applications you can visit the following pages:
Hopefully you now have a better sense of the signal processing workflow for deep learning, and the tools we offer to enable it and make it easier.
Have any questions about signal processing for deep learning? Leave a comment below.
 The larger and higher quality the dataset, the closer you can get to being able to perform deep learning with raw signal data. Similarly, if you have higher computational power, you will be able to train more complex networks that will improve performance.
On the other hand, if you understand your data, you may be successful extracting key features to feed into a traditional machine learning algorithm without the need of a large dataset and of a deep network. This requires more signal processing knowledge, but results can be impressive.
Between the two extremes of raw signal data and crafting a customized machine learning approach are some interesting considerations:
The larger and higher quality the dataset, the closer you can get to being able to perform deep learning with raw signal data. Similarly, if you have higher computational power, you will be able to train more complex networks that will improve performance.
On the other hand, if you understand your data, you may be successful extracting key features to feed into a traditional machine learning algorithm without the need of a large dataset and of a deep network. This requires more signal processing knowledge, but results can be impressive.
Between the two extremes of raw signal data and crafting a customized machine learning approach are some interesting considerations:
 Next we’ll walk through each of these steps, addressing what to do when:
Next we’ll walk through each of these steps, addressing what to do when:
 Phased Array System Toolbox offers functionality to model micro-doppler radar signatures of pedestrians (new in 19a) that can be used in automated driving applications.
Phased Array System Toolbox offers functionality to model micro-doppler radar signatures of pedestrians (new in 19a) that can be used in automated driving applications.
 There are other apps as well, including:
There are other apps as well, including:
 There are a variety of spectral functions to measure power, bandwidth and harmonics.
There are a variety of spectral functions to measure power, bandwidth and harmonics.
 And there are time-frequency transformation functions, from continuous wavelet transform, to Wigner-Ville distribution and short-time Fourier transform, which are commonly used in deep learning applications.
You can choose the transform that best suits your time and frequency resolution needs.
And there are time-frequency transformation functions, from continuous wavelet transform, to Wigner-Ville distribution and short-time Fourier transform, which are commonly used in deep learning applications.
You can choose the transform that best suits your time and frequency resolution needs.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building












コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。