Optimal Fit of a Non-linear Function

This is a demonstration of the optimal fitting of a non-linear function to a set of data. It uses FMINSEARCH, an implementation of the Nelder-Mead simplex (direct search) algorithm, to minimize a nonlinear function of several variables.

This M-file is a function, which will let us use a nested function.

function fitdemonew

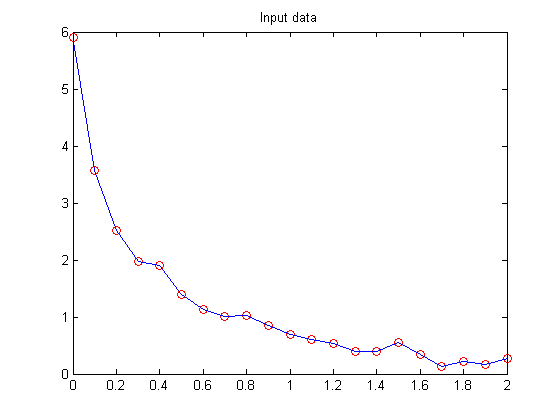
Create some sample data and plot it.

t = (0:.1:2)';
y = [5.8955 3.5639 2.5173 1.9790 1.8990 1.3938 1.1359 1.0096 1.0343 ...
    0.8435 0.6856 0.6100 0.5392 0.3946 0.3903 0.5474 0.3459 0.1370 ...
    0.2211 0.1704 0.2636]';
plot(t,y,'ro'); hold on; h = plot(t,y,'b'); hold off;
title('Input data'); ylim([0 6])

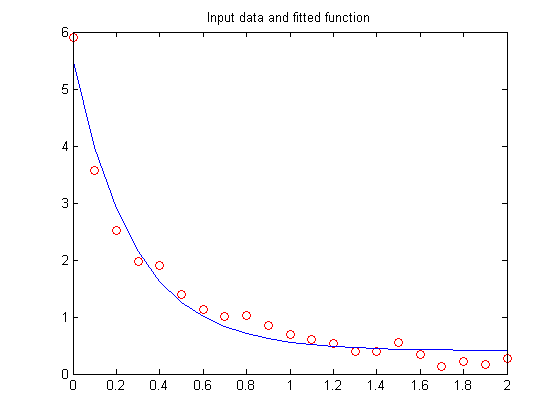
The goal is to fit the following function with two linear parameters and two nonlinear parameters to the data:

   y =  C(1)*exp(-lambda(1)*t) + C(2)*exp(-lambda(2)*t)

To fit this function, we've create a function FITFUN. Given the nonlinear parameter (lambda) and the data (t and y), FITFUN calculates the error in the fit for this equation and updates the line (h).

    function err = fitfun(lambda,t,y)
        A = zeros(length(t),length(lambda));
        for j = 1:length(lambda)
            A(:,j) = exp(-lambda(j)*t);
        end
        c = A\y;
        z = A*c;
        err = norm(z-y);
    end

Make a guess for initial estimate of lambda (start) and invoke FMINSEARCH. It minimizes the error returned from FITFUN by adjusting lambda. It returns the final value of lambda. Use an output function to plot intermediate fits.

start = [1;0];
% We use an anonymous function to pass additional parameters t, y, h to the
% output function.
outputFcn = @(x,optimvalues,state) fitoutputfun(x,optimvalues,state,t,y,h);
options = optimset('OutputFcn',outputFcn,'TolX',0.1);
estimated_lambda = fminsearch(@(x)fitfun(x,t,y),start,options)

estimated_lambda =

    3.5897
    0.0030

end