Why “Where’s Waldo”?
Today I'd like to introduce guest blogger Seth DeLand who works for the MATLAB Product Marketing team here at MathWorks. Today, Seth will be discussing some different optimization techniques that he used for developing a strategy for the puzzle-books "Where's Waldo?".
Contents
There was a nice post on Randal Olson’s blog last week about techniques for the popular puzzle-books “Where's Waldo?” (originally “Where’' Wally?” in the UK).
As a kid, I spent hours going through my collection of Where's Waldo? books, so I was inspired by Randal's post to do some of my own analysis. It would be great if I could show that in the last 20 years, I’ve learned enough to have a little better strategy for finding Waldo.
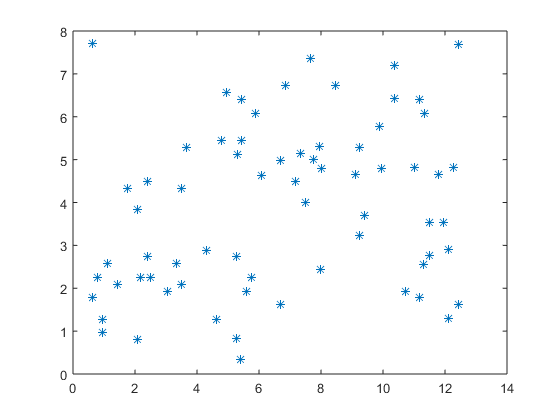
I started by grabbing the data for the Waldo locations in every book, and plotting the points:
pts = webread('http://www.randalolson.com/wp-content/uploads/wheres-waldo-locations.csv'); plot(pts.X,pts.Y,'*');
Finding the shortest path
The next thing I wanted to do was try to reproduce some of Randal’s results. The traveling salesman problem (What is the shortest path that goes through all of the points?) is always fun to dig into. I used the same start and end points for my path as in the original post, but took a different approach for finding the solution. Instead of using a genetic algorithm, I chose to formulate this as a binary programming problem, similar to what is done in this example. This approach has 2 advantages:
- It's really fast for problems of this size (on the order of 100 stops)
- We can prove we’ve actually found the shortest possible path
Let's look at the results:
[order,pathLength,output] = shortestPathAToB([pts.X pts.Y],1,67);
hold on
plot(pts.X(order),pts.Y(order))

Examining the output from the INTLINPROG optimization solver, we see that the Absolute Gap is 0, meaning we have found the shortest possible path.
output.absolutegap
ans =
0
A different take on the shortest path
Solving the traveling salesman problem is nice, but when you’re actually searching for Waldo you’re looking at a region instead of a point. It’s kind of like you’re applying a circular mask to the page, and you can see everything within that circle. So this got me thinking: what if we tried to find the shortest path, such that if you translated a circle of radius “r” along that path, you would cover all of the Waldo locations? This makes the problem a bit more complex, since we have to compute distances from all of the Waldo locations to arbitrary line segments making up the path.
I chose to formulate it as a nonlinear programming problem, where again the objective is to minimize the total distance, and we add a nonlinear constraint that says all of the Waldo points must be within “r” of some point on the path. The solution from the last problem serves as a good starting point. We then have enough to turn FMINCON loose on the problem. To make things interesting, I solved for 4 different values of “r”.
r = 0.25:0.25:1; pts = pts(order,:); npts = length(pts.X); x0 = [pts.X; pts.Y]; % Initial guess at solution lb = zeros(2*npts,1); % All variables >= 0 ub = [13*ones(npts,1); 8*ones(npts,1)]; % x-variables are <= 13, y-variables are <= 8 options = optimoptions('fmincon',... 'Algorithm','sqp',... 'Display','none',... 'TolFun',1E-3,... 'MaxFunEvals',1E5); xopt = zeros(length(x0),length(r)); fval = zeros(1,length(r)); parfor i = 1:length(r) noncon = @(x) nonlcon(x,[pts.X,pts.Y],r(i)); [xopt(:,i),fval(i)] = fmincon(@objfcn,x0,[],[],[],[],lb,ub,noncon,options); end figure; for i = 1:length(r) subplot(2,2,i); drawPath(xopt(:,i),pts,r(i)); title({['View Radius = ' num2str(r(i))]; ... ['Path Length = ' num2str(fval(i))]}); end

Analyzing the solution
As expected, as the value of “r” increases, the length of the path decreases. Here’s an animation of what it would look like traversing this path for a view radius of 1:
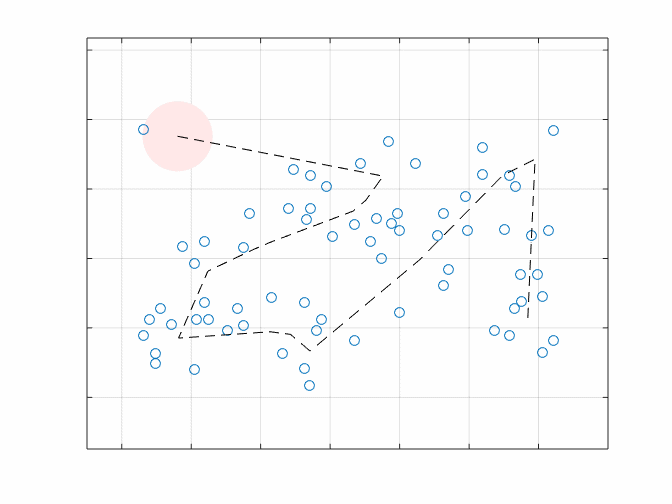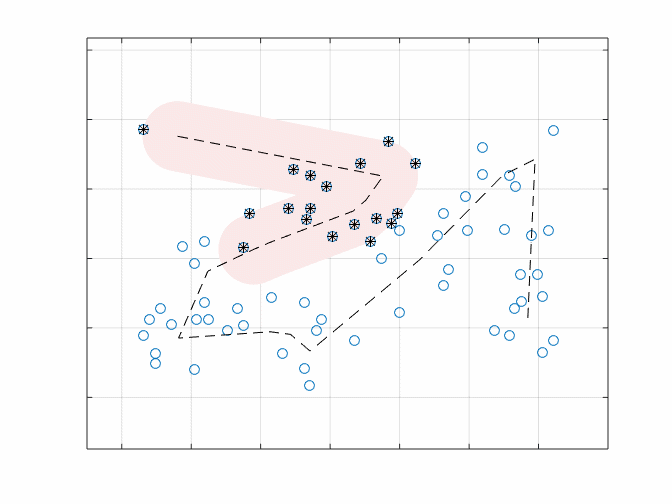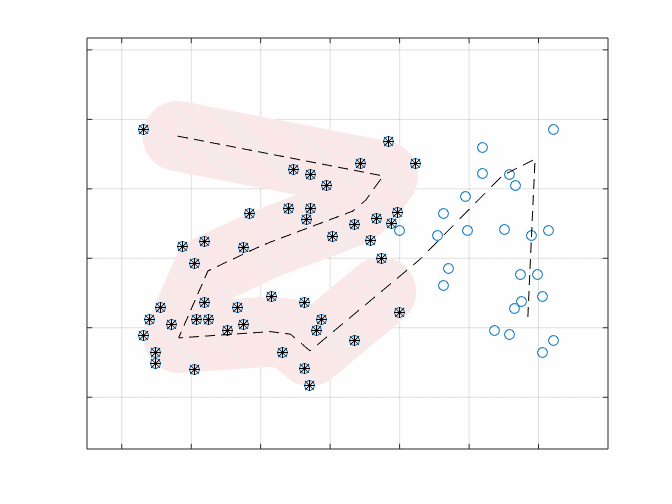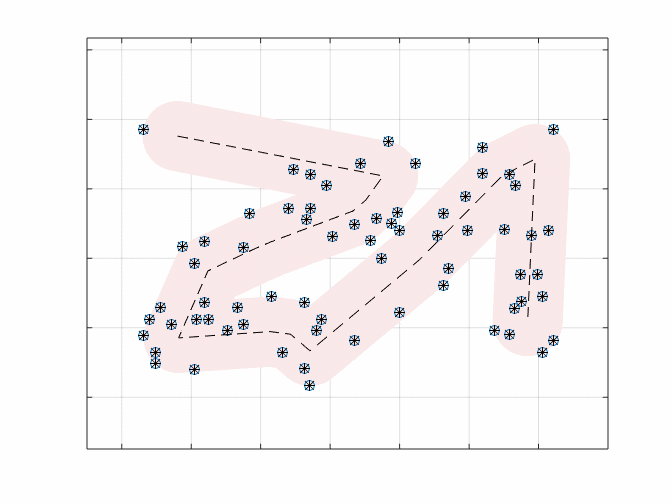
The path length shrinks from a length of 58.8 when we explicitly visit each stop, to 31.2 when we have a radius of 1. So we have managed to shorten our search path by quite a bit. Looking at the path, I would describe it as a Z then an uppercase Lambda, or:
$$Z\Lambda$$
That makes it easy enough to remember. All of the code I used for this analysis is available in this GitHub repository.
Who has a different idea for finding Waldo? Have any of you image processing gurus tried tackling this problem? Let us know here.
- Category:
- Fun,
- Optimization
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.