How to Compute Perceptual Color Difference
I wrote previously about the new colorChecker, which can detect X-Rite test charts in the R2020b release. Another area of new color-related functionality is computing perceptual color differences. There is the new function deltaE, which computes color differences based on the L*a*b* color space and the CIE76 standard. There is also the imcolordiff function, which can compute color differences based either on the CIE94 or the CIEDE2000 standard.
I recently mentioned to someone on the Image Processing Toolbox team that I was planning to write a blog post about these functions, and he posed the following question: which two colors are the furthest apart, perceptually speaking? I decided to give that a try using $\Delta_E$. I'll formulate the problem this way: which two sRGB colors have the largest $\Delta_E$ between them?
In a related post back in 2015, I demonstrated how to plot the sRGB gamut surface in L*a*b* space, like this:
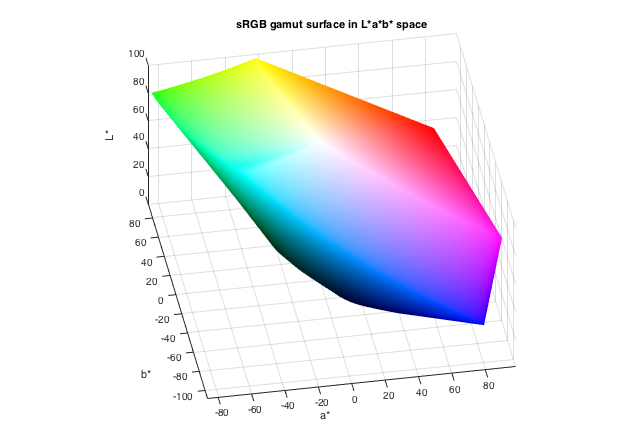
Looking at this diagram, you might be able to guess the answer. But, let's work through it. The first thing I want to do is to sample the sRGB space.
[r,g,b] = ndgrid(linspace(0,1,100)); rgb = [r(:), g(:), b(:)];
Next, convert the sRGB colors to Lab. (I'm going to stop typing the "*" characters.)
lab = rgb2lab(rgb);
Now let's find the colors on the convex hull of the Lab values. The pair of colors most distant from each other must both be on the convex hull.
k = convhull(lab); hull_colors = lab(unique(k(:,1)),:);
If this were a two-dimensional problem, then I know of an algorithm that can find the most distant pair of points in $O(N)$, where $N$ is the number of points on the convex hull. I don't know of a similar algorithm in three dimensions, so I'm just going to brute force it by computing the distance between every color pair.
So, how many colors are we talking about?
size(hull_colors)
ans =
3980 3
There are 3908 colors, each of which is represented by a 3-element vector in Lab space. The color difference $\Delta_E$ is the Euclidean distance between two colors in Lab space. I want to compute the distance between every color in that set and every other color. Here is a nifty and compact way to do that using the implicit expansion behavior of MATLAB arithmetic operators.
C1 = reshape(hull_colors,[],1,3); C2 = reshape(hull_colors,1,[],3); Cdiff = C1 - C2; DE = sqrt(sum(Cdiff.^2,3)); size(DE)
ans =
3980 3980
You can see that DE is an 3980x3980 matrix. It contains the pair-wise distances between all the convex hull colors. (See also pdist2, a function in the Statistics and Machine Learning Toolbox that can compute pair-wise vector distances with much more flexibility, as well as hypot, a MATLAB function that computes the magnitude of a two-element vector in a way that avoids numerical overflow and underflow problems.)
Let's find where the maximum distances are in this matrix.
[m,n] = find(DE == max(DE(:)))
m =
3883
92
n =
92
3883
What are those colors (in Lab space)?
max_colors_lab = hull_colors(m,:)
max_colors_lab = 32.2970 79.1875 -107.8602 87.7347 -86.1827 83.1793
And those two colors in sRGB space:
max_colors_rgb = lab2rgb(max_colors_lab)
max_colors_rgb =
0.0000 -0.0000 1.0000
0.0000 1.0000 0.0000
They are just the sRGB green and blue primaries.
colorSwatches(max_colors_rgb) axis equal axis off

(colorSwatches is a DIPUM3E function that is available to you in MATLAB Color Tools on the File Exchange and on GitHub.)
These two colors have a $\Delta_E$ of:
DE(m(1),n(1))
ans = 258.6827
The deltaE function offers a more convenient way to compute $\Delta_E$:
deltaE([0 1 0],[0 0 1])
ans = 258.6827
Some other time, I will write about the other color difference calculations provided by imcolordiff.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.