Separable convolution: Part 2
Back in October I introduced the concept of filter separability. A two-dimensional filter s is said to be separable if it can be written as the convolution of two one-dimensional filters v and h:

I said then that "next time" I would explain how to determine whether a given filter is separable. Well, I guess I got side-tracked, but I'm back on topic now.
This question gave me one of earliest opportunities at The MathWorks to wander down to company co-founder Cleve's office and ask for advice. I asked, "How can I determine if a matrix is an outer product of two vectors?" Cleve was very helpful, as he always is, although I was a little embarrassed afterward that I hadn't figured it out myself. "Go look at the rank function," Cleve told me.
Of course. If a matrix is an outer product of two vectors, its rank is 1. Here are the key lines of code in rank:
dbtype 15:19 rank
15 s = svd(A); 16 if nargin==1 17 tol = max(size(A)') * eps(max(s)); 18 end 19 r = sum(s > tol);
So the test is this: The rank of A is the number of nonzero singular values of A, with some numerical tolerance based on eps and the size of A.
Let's try it with a few common filters.
An averaging filter should be obvious:
averaging = ones(5,5) / 25; rank(averaging)
ans =
1
The Sobel kernel:
sobel = [-1 0 1; -2 0 2; -1 0 1]; rank(sobel)
ans =
1
The two-dimensional Gaussian is the only radially symmetric function that is also separable:
gaussian = fspecial('gaussian');
rank(gaussian)
ans =
1
A disk is not separable:
disk = fspecial('disk');
rank(disk)
ans =
5
So how can we determine the outer product vectors? The answer is to go back to the svd function. Here's a snippet from the doc: [U,S,V] = svd(X) produces a diagonal matrix S of the same dimension as X, with nonnegative diagonal elements in decreasing order, and unitary matrices U and V so that X = U*S*V'.
A rank 1 matrix has only one nonzero singular value, so U*S*V' becomes U(:,1) * S(1,1) * V(:,1)'. This is basically the outer product we were seeking. Therefore, we want the first columns of U and V. (We have to remember also to use the nonzero singular value as a scale factor.)
Let's try this with the Gaussian filter.
[U,S,V] = svd(gaussian)
U =
-0.1329 0.9581 -0.2537
-0.9822 -0.1617 -0.0959
-0.1329 0.2364 0.9625
S =
0.6420 0 0
0 0.0000 0
0 0 0.0000
V =
-0.1329 -0.6945 -0.7071
-0.9822 0.1880 0.0000
-0.1329 -0.6945 0.7071
Now get the horizontal and vertical vectors from the first columns of U and V.
v = U(:,1) * sqrt(S(1,1))
v = -0.1065 -0.7870 -0.1065
h = V(:,1)' * sqrt(S(1,1))
h = -0.1065 -0.7870 -0.1065
I have chosen, somewhat arbitrarily to split the scale factor, S(1,1), "equally" between v and h.
Now check to make sure this works:
gaussian - v*h
ans = 1.0e-015 * -0.0243 -0.1527 -0.0243 -0.0139 -0.1110 -0.0139 -0.0035 0 -0.0035
Except for normal floating-point roundoff differences, gaussian and v*h are equal.
You can find code similar to this in the MATLAB function filter2, as well as in the Image Processing Toolbox function imfilter.




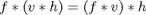




コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。