Building an Optimization Agent with MATLAB MCP Core Server

作者 Yann Debray, January 26, 2026

120 次查看（过去 30 天） | 0 个赞 | 0 个评论

Co-author: Tom Couture

Tom Couture is the Product Manager for Optimization. In this blog post, he joins me to demonstrates how to use the new MATLAB MCP Core Server to build optimization agents.

If you are like Tom, you have probably spent hours setting up optimization problems in MATLAB—defining objective functions, constraints, choosing solvers, tweaking options. Now, what if I told you that you can have a conversation with an AI agent that does all of this for you, like a mini Tom in your pocket, while actually running the optimization in your local MATLAB?

That is where the MATLAB MCP Core Server comes in, combined with the powerful Optimization Toolbox™. In this post, we are going to walk you through how to create an optimization agent that can solve real engineering problems—from simple constrained optimization to computationally expensive CFD-based design optimization using surrogate models.

The First Thing Your Agent Should Do: Check the Toolboxes

One of the first features of the MATLAB MCP Core Server I demo is the detect_matlab_toolboxes tool. Before your agent starts writing optimization code, it should verify that you have the necessary toolboxes installed.

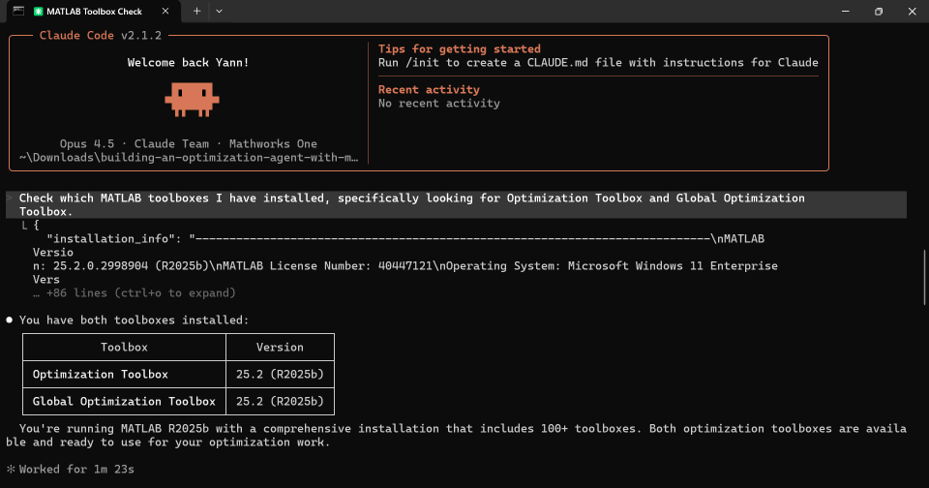
Here is a sample prompt to your AI assistant (Claude Desktop®, GitHub Copilot®, or any MCP-compatible client):

"Check which MATLAB toolboxes I have installed, specifically looking for Optimization Toolbox and Global Optimization Toolbox."

The agent will call the detect_matlab_toolboxes tool and return something like:

Optimization Toolbox - Version 25.2 (R2025b) ✓

Global Optimization Toolbox - Version 25.2 (R2025b) ✓

This is crucial because the solver you can use depends entirely on what you have licensed. No Optimization Toolbox? The agent will know to fall back to fminsearch. Have Global Optimization Toolbox? Great, surrogateopt is on the table for those expensive simulations.

Example 1: Structural Beam Design Optimization

Let me demo to you a classic engineering optimization problem: designing a cantilever beam for minimum weight while satisfying stress and deflection constraints.

The Problem

We want to minimize the weight of a rectangular cross-section beam subject to:

Maximum stress constraint (must not exceed yield strength)
Maximum deflection constraint (must not exceed allowable deflection)
Bounds on width and height

Here is the prompt I gave to Claude Code:

"I need to optimize a cantilever beam design. The beam has length L=5m, carries a tip load P=10kN, made of steel with E=200 GPa and yield stress=250 MPa. I want to minimize the cross-sectional area (width × height) while keeping tip deflection under 10mm and max stress under the yield stress. Width should be between 50-200mm, height between 100-500mm. Please set this up and solve it using MATLAB."

The agent generated and ran the following code:

% Beam optimization problem

L = 5; % Length [m]

P = 10000; % Tip load [N]

E = 200e9; % Young's modulus [Pa]

sigma_yield = 250e6; % Yield stress [Pa]

delta_max = 0.010; % Max deflection [m]

% Objective: minimize cross-sectional area

objective = @(x) x(1) * x(2); % width * height

% Nonlinear constraints

nonlcon = @(x) beamConstraints(x, L, P, E, sigma_yield, delta_max);

% Bounds: [width_min, height_min] to [width_max, height_max]

lb = [0.05, 0.10]; % [m]

ub = [0.20, 0.50]; % [m]

% Initial guess

x0 = [0.10, 0.25];

% Solve

options = optimoptions('fmincon', 'Display', 'iter', 'Algorithm', 'sqp');

[x_opt, fval, exitflag] = fmincon(objective, x0, [], [], [], [], lb, ub, nonlcon, options);

fprintf('Optimal width: %.1f mm\n', x_opt(1)*1000);

fprintf('Optimal height: %.1f mm\n', x_opt(2)*1000);

fprintf('Optimal area: %.2f cm²\n', fval*1e4);

The constraint function:

function [c, ceq] = beamConstraints(x, L, P, E, sigma_yield, delta_max)

 b = x(1); % width

 h = x(2); % height

 I = b * h^3 / 12; % Second moment of area

 sigma = P * L * (h/2) / I; % Max bending stress

 delta = P * L^3 / (3 * E * I); % Tip deflection

 c(1) = sigma - sigma_yield; % Stress constraint

 c(2) = delta - delta_max; % Deflection constraint

 ceq = [];

end

The result? An optimal beam with width 80.2mm and height 189.4mm—satisfying both constraints at the boundary, which is exactly what you would expect from a well-posed optimization problem.

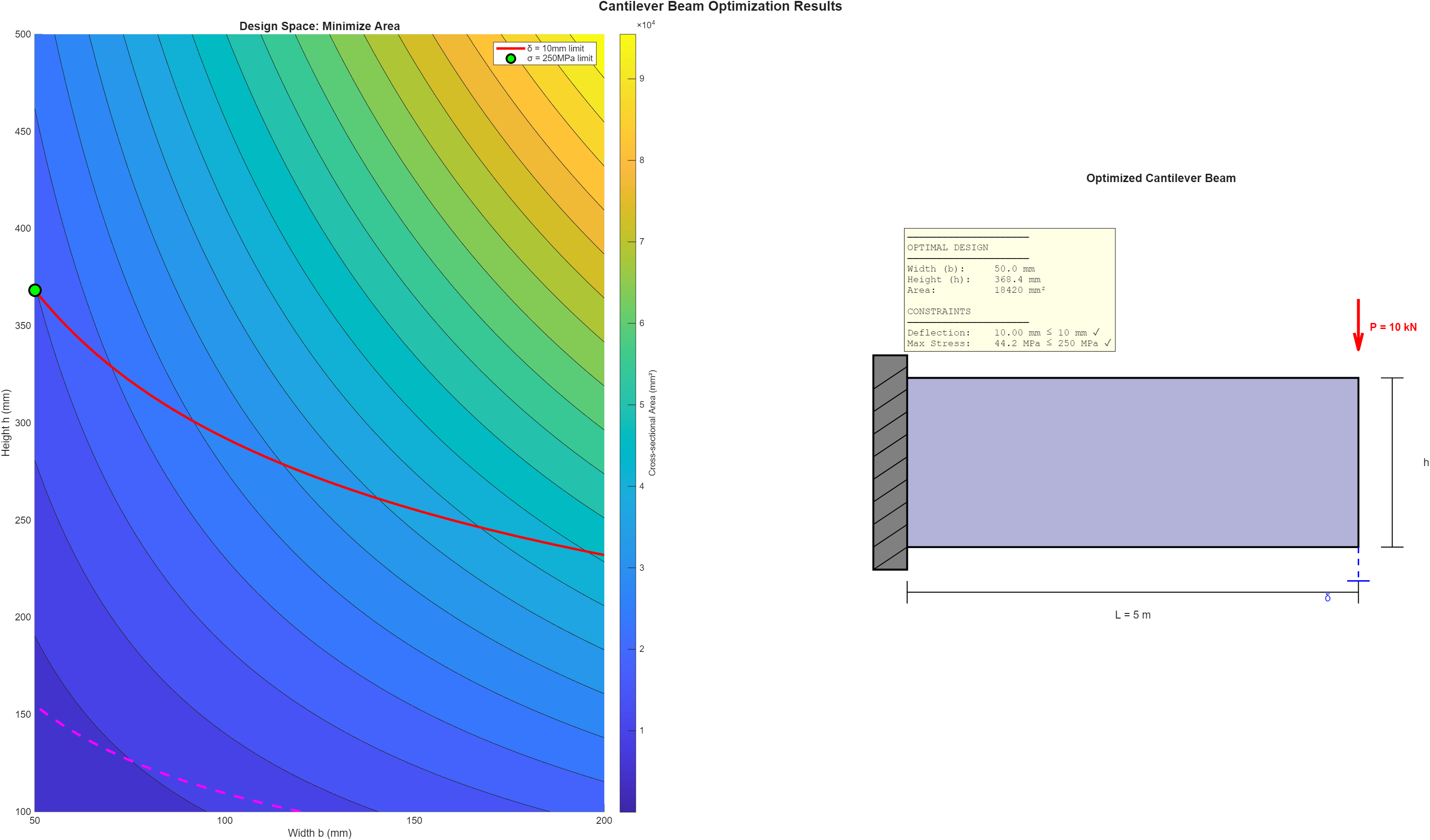
You can take a look at my conversation with Claude to see some of the rationale as to why he used a fmincon solver for this problem:

https://mathworks.github.io/MATLAB-AI-Blog/optimization-agent/claude/

In the repo, I'm also sharing a "skill" for a problem-based approach:

https://github.com/mathworks/MATLAB-AI-Blog/blob/main/optimization-agent/.claude/skills/problem-based-optim/SKILL.md

Example 2: CFD-Based Optimization with Response Surfaces

Now let's get to the fun part. One of my favorite applications of optimization in MATLAB is when you have a computationally expensive simulation—like CFD—and you need to find optimal design parameters.

The Lid-Driven Cavity Problem

The lid-driven cavity is the "Hello World" of CFD. It is a square cavity where the top wall (the "lid") moves at a constant velocity, and you solve the Navier-Stokes equations to find the flow field. For this demo, I will be using an implementation from this problem in pure MATLAB from my colleague Michio in Japan. The code can be found on GitHub: 2D Lid-Driven Cavity Flow Solver

The question I posed to the agent:

"I have a CFD solver in the folder 2D-Lid-Driven-Cavity-Flow-Incompressible-Navier-Stokes-Solver. I want to
optimize the lid velocity and Reynolds number to minimize the maximum vorticity in the secondary corner vortex of
a lid-driven cavity flow. Reynolds number should be between 100 and 1000, and lid velocity between 0.5 and 2.0
m/s."

Why Surrogate Optimization?

If you have tried running fmincon on a CFD objective function, you know the pain. Each function evaluation takes 30 seconds, and gradient-based methods might need hundreds of evaluations. surrogateopt from the Global Optimization Toolbox is designed exactly for this scenario:

What's New	Why It Matters
Builds a surrogate (response surface) of your expensive function	Fewer actual CFD simulations needed
Uses Radial Basis Function interpolation	Accurately approximates complex surfaces
Global search capability	Doesn't get stuck in local minima
Supports parallel evaluation	Use all your CPU cores

Here is the code the agent generated:

% Define bounds

lb = [100, 0.5]; % [Re_min, V_min]

ub = [1000, 2.0]; % [Re_max, V_max]

% Set up surrogate optimization

options = optimoptions('surrogateopt', ...

'Display', 'iter', ...

'PlotFcn', 'surrogateoptplot', ...

'MaxFunctionEvaluations', 50, ...

'MinSurrogatePoints', 20);

% Run optimization

[x_opt, fval, exitflag, output] = surrogateopt(@cavityObjective, lb, ub, options);

fprintf('Optimal Reynolds number: %.0f\n', x_opt(1));

fprintf('Optimal lid velocity: %.2f m/s\n', x_opt(2));

fprintf('Minimum corner vorticity: %.4f\n', fval);

The objective function:

function obj = cavityObjective(x)

 Re = x(1);

 V_lid = x(2);

% Run CFD simulation (using 2D-Lid-Driven-Cavity solver)

 [u, v] = runCavitySimulation(Re, V_lid);

% Calculate vorticity in corner region

 [vorticity] = calculateVorticity(u, v);

% Extract max vorticity in secondary vortex region

 cornerRegion = vorticity(1:20, 1:20);

 obj = max(abs(cornerRegion(:)));

end

The beauty of surrogateopt is that it builds a response surface as it goes. After just 20 function evaluations (about 5 minutes), it found the optimal operating point—something that would have taken hours with a grid search.

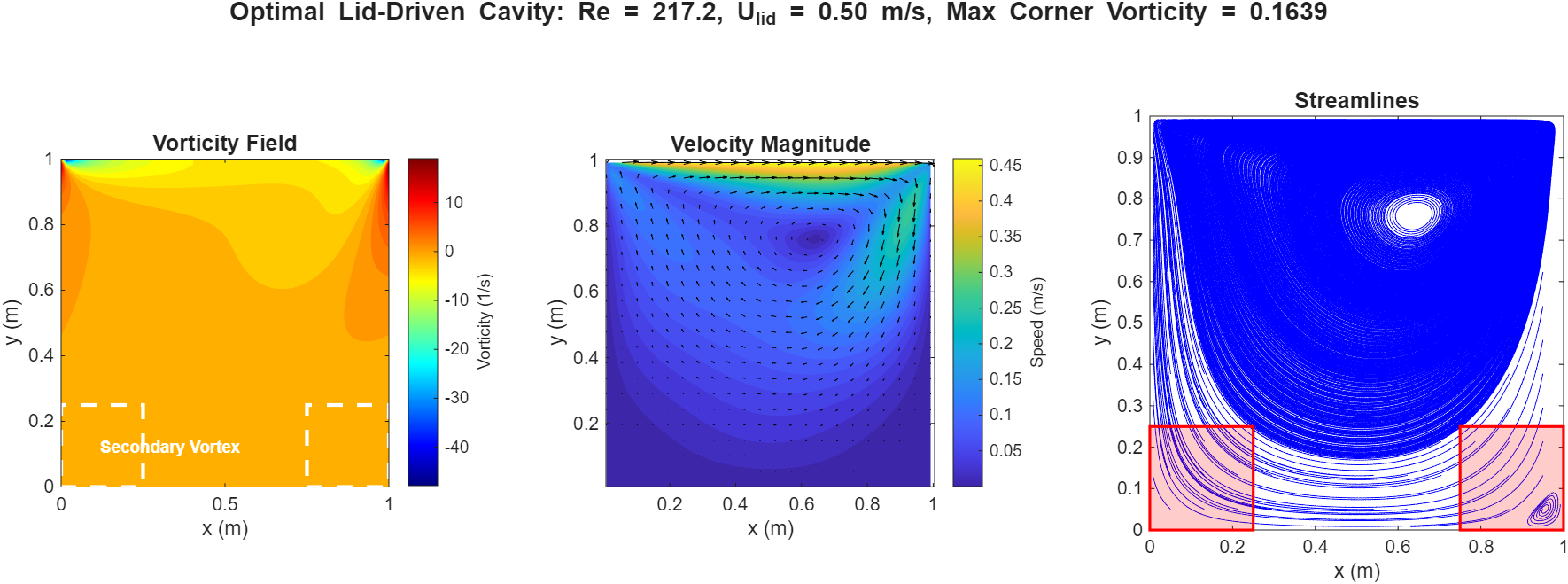
What's Next?

The combination of MATLAB MCP Core Server + Optimization Toolbox opens up a whole new way of doing engineering optimization. Instead of context-switching between documentation, code editor, and command window, you can have a conversation with an AI that:

Checks your toolboxes to know what solvers are available
Formulates the problem based on your natural language description
Writes and runs the code in your local MATLAB
Iterates on errors without you copying and pasting

If you want to try this yourself, head over to the MATLAB MCP Core Server repository and follow the setup instructions. The server provides five core tools—but combined with the 100+ functions in Optimization Toolbox, the possibilities are endless.