Game of Life, Part 3, Sampler
The Game of Life. A few more of my favorite populations.
Contents
The R-pentomino
There are 12 different five-cell starting populations. Conway named them pentominos and distinguished them by the letter of the alphabet that they vaguely resembled. He was able to establish by hand that 11 of them stabilize in at most 10 generations, but without a computer he was unable to determine the fate of the R-pentomino.
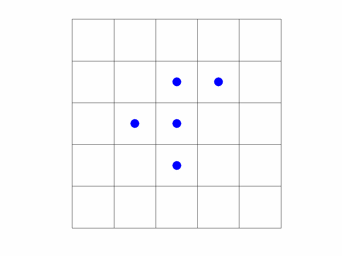
It turns out to take 1103 steps to stabilize, by which time it has spawned a half dozen gliders and reached a population of 116. Here is a movie showing every tenth step of 1200 steps. R-pentomino-movie.
Gliders by the Dozen
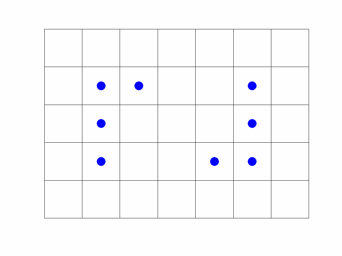
This position stabilizes at step 184. Here is every fourth step for 300 steps. Gliders-by-the-dozen-movie.
Canada Goose
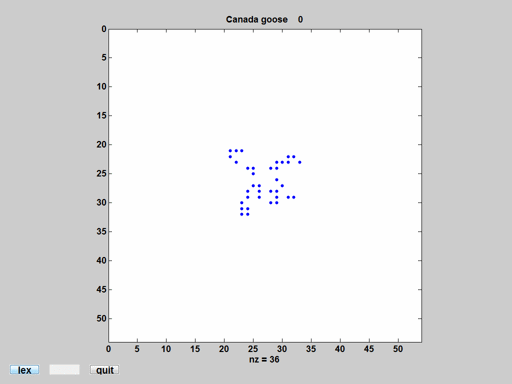
At the time of its discovery in 1999, this was the smallest known diagonal spaceship other than the glider. Here is every tenth step for a thousand steps. Canada-Goose-movie.
Washerwoman
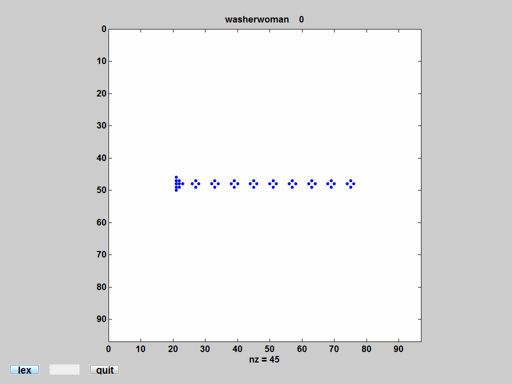
This represents a group of populations known as fuses. Here is every third step for 270 steps. Washerwoman-movie.
Spacefiller
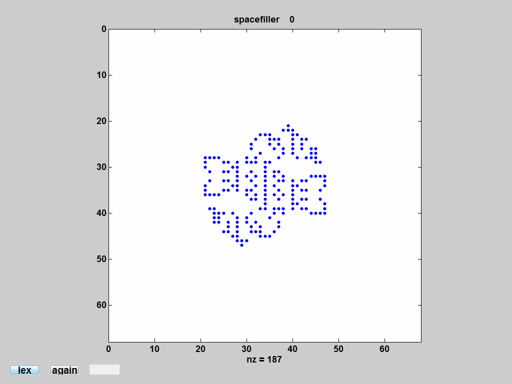
As the name implies, the spacefiller fills all of space. The number of nonzeros in the sparse matrix increases quadratically with the time step, so the data structure is not efficient in this situation. spacefiller-movie.
R2D2
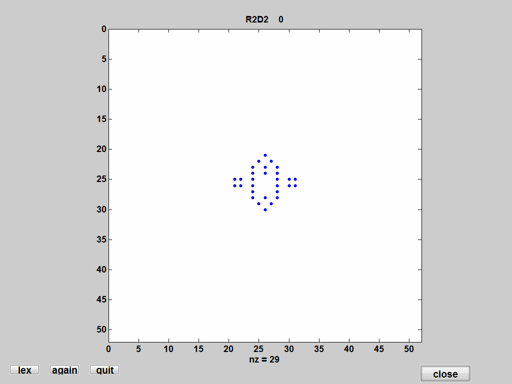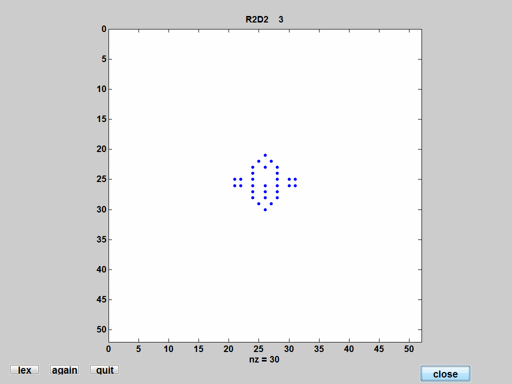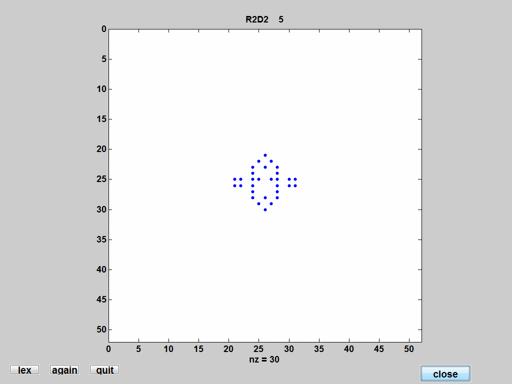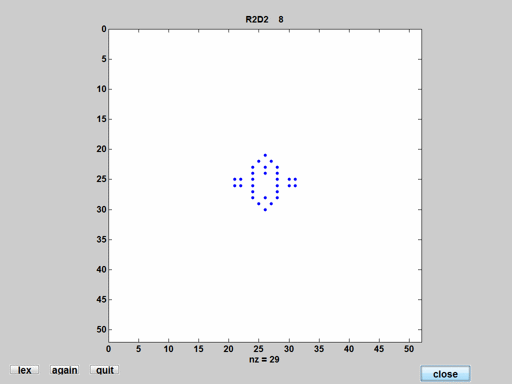
The droid from Star Wars. Sometimes simpler is better. We don't need a movie here.
L_logo
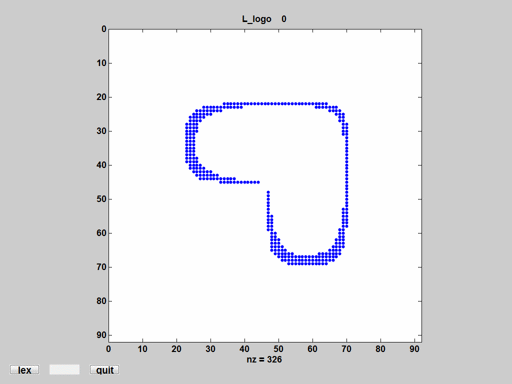
This is not from the Lexicon. Our finale is the Game of Life initialed with a contour from the MathWorks logo. After creating 12 gliders, it stabilizes at time 2637 with a population of 636. L_logo_movie
% L = membrane(1,25,9,9); % U = sparse(91,91); % U(21:71,21:71) = L; % S = .05<U & U<.15; % spy(S) % life_lex(S)
- 类别:
- Matrices








评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。