Anatomy of a Cube

作者 Cleve Moler, January 3, 2022

10 次查看（过去 30 天） | 0 个赞 | 3 个评论

A cube is the familiar three-dimensional solid with eight vertices, six faces and twelve edges. I have been working with cubes recently in posts about both the Menger sponge fractal and the 4-by-4 matrix from computer graphics.

Vertices
Edges
Wireframe
Faces

Vertices

Cartesian coordinates, V, for the eight vertices of a cube can be generated from the binary representation of 0:7.

    j = (0:7)'

    k = dec2bin(j)

k =

  8×3 char array

    '000'
    '001'
    '010'
    '011'
    '100'
    '101'
    '110'
    '111'

    V = double(k-'0')

V =

     0     0     0
     0     0     1
     0     1     0
     0     1     1
     1     0     0
     1     0     1
     1     1     0
     1     1     1

Edges

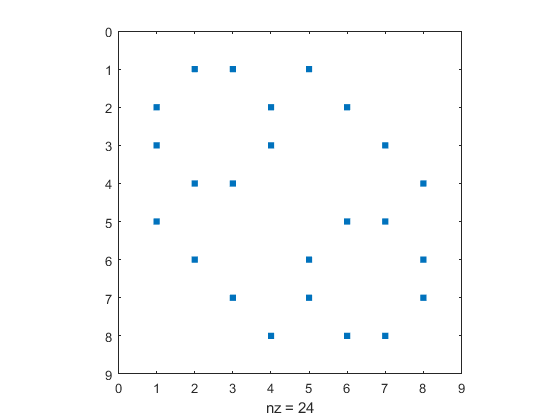
The twelve edges of a cube are described by the adjacency matrix A of connections between its vertices.

    A = adjacency(V)
    spy(A)

A =

     0     1     1     0     1     0     0     0
     1     0     0     1     0     1     0     0
     1     0     0     1     0     0     1     0
     0     1     1     0     0     0     0     1
     1     0     0     0     0     1     1     0
     0     1     0     0     1     0     0     1
     0     0     1     0     1     0     0     1
     0     0     0     1     0     1     1     0

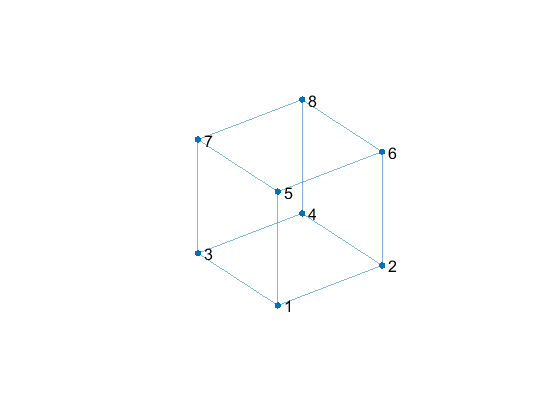
Wireframe

A plot of the graph of A provides a wireframe view of our cube.

    G = graph(A);
    p = plot(G, ...
        NodeLabel = string(k), ...
        NodeFontSize = 12, ...
        XData = V(:,3), ...
        YData = V(:,2), ...
        ZData = V(:,1));

    axis([-1 4 -1 4 -1 4]/3)
    axis square off vis3d
    view(3)

Let's replace the node labels with 1-based indices for rows of V.

p.NodeLabel = string(j+1);

Faces

A cube has six square faces. This array F provides the indices in V of the coordinates of the corners of each face. The ordering ensures that the normal to each face points out of the cube.

    F = [ 1 5 7 3
          3 7 8 4
          1 3 4 2
          2 4 8 6
          1 2 6 5
          5 6 8 7 ]

F =

     1     5     7     3
     3     7     8     4
     1     3     4     2
     2     4     8     6
     1     2     6     5
     5     6     8     7

If you Google "rgb gold", you will get links to Web sites offering red-green-blue values for dozens of shades of the color gold. My forthcoming post about the complement of the Menger sponge fractal uses just two shades.

    gold = [212 175 55]/256
    dark = gold/2

gold =

    0.8281    0.6836    0.2148


dark =

    0.4141    0.3418    0.1074

The single patch formed from V and F is just the skin enclosing our cube; its inside is hollow.

    cla
    patch(Faces = F, ...
        Vertices = V, ...
        FaceColor = gold, ...
        EdgeColor = dark, ...
        LineWidth = 1.5);

    axis([-1 4 -1 4 -1 4]/3)
    axis square off vis3d
    view(3)