Shortly after I published the second post about the Mertens conjecture, a reader's comment suggested a new approach to computing Redheffer determinants and the Mertens function. It is now possible to compute a half-million values of the Mertens function in about five hours.

Contents

Block matrices

The comment references the Wikipedia article on block matrices.

  You could also consider the matrix as a 2x2 block matrix and
  use the formula for the determinant of a block matrix [1].
      A = redheffer(n);
      M = full(A(1,1) - A(1, 2:end) * (A(2:end,2:end) \ A(2:end, 1)));
  Since the (n-1)x(n-1) block is upper triangular, the solve becomes
  a back-substitution.

redmert

My new program is named redmert, an abbreviation of Redheffer-Mertens. It uses the fact that redheffer(n) is obtained from redheffer(n-1) by appending the last column.

Let R(n) denote the upper or right-triangular part of redheffer(n).

  R(n) = triu(redheffer(n))

R(n) is sparse, upper triangular and has ones on the diagonal. The indices of the nonzeros in the last column of R(n) are the factors of n. For example, here is R(8).

R8 = full(triu(redheffer(8)))

R8 =
     1     1     1     1     1     1     1     1
     0     1     0     1     0     1     0     1
     0     0     1     0     0     1     0     0
     0     0     0     1     0     0     0     1
     0     0     0     0     1     0     0     0
     0     0     0     0     0     1     0     0
     0     0     0     0     0     0     1     0
     0     0     0     0     0     0     0     1

The idea behind redmert is to compute a sequence of Redheffer matrices, R, and associated values of the Mertens function, M.

  [M,R] = redmert(p,R)

The input is a scalar integer p, the desired sequence length, and a sparse matrix R, the upper triangle of a Redheffer matrix of some order, n. The output is an integer vector of values M(n+1:n+p) and the upper triangle of the Redheffer matrix of order n+p. This output R can then be used as the input R in another call to redmert.

The sequence is started with an empty R.

For example,

[M,R] = redmert(8,[]);

The output is mertens(n), n = 1:8, and R8 from the example above.

MR8 = full(R)

M =
     1
     0
    -1
    -1
    -2
    -1
    -2
    -2
R8 =
     1     1     1     1     1     1     1     1
     0     1     0     1     0     1     0     1
     0     0     1     0     0     1     0     0
     0     0     0     1     0     0     0     1
     0     0     0     0     1     0     0     0
     0     0     0     0     0     1     0     0
     0     0     0     0     0     0     1     0
     0     0     0     0     0     0     0     1

Inside redmert

The entire code for redmert is twelve lines long. It manipulates sparse matrices and uses sparse backslash to solve a triangular system. Nothing else is required.

Lines 7 and 8 generate the last column of R and lines 9 and 10 implement the new idea about block matrices.

dbtype redmert

1     function [M,R] = redmert(p,Rin)
2         M = zeros(p,1);
3         R = sparse(triu(Rin));
4         n = size(R,1);
5         for q = 1:p
6             n = n+1;
7             k = (mod(n,1:n) == 0);
8             R(k,n) = 1;
9             e = ones(n-1,1);
10            M(q) = R(1,1) - e'*(R(2:n,2:n)\e);
11        end
12    end

mertens_plot

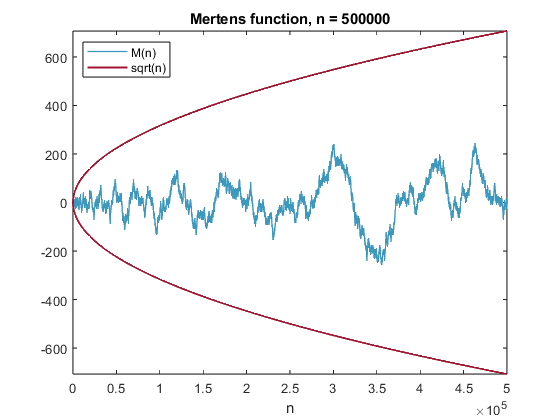
It takes about five hours for redmert to compute half a million values on my laptop.

   n = 0.5e6;
   p = 0.5e4;
   R = sparse([]);
   M = [];
   for k = p:p:n
       disp(k)
       [Mout,R] = redmert(p,R);
       M = [M; Mout];
       mertens_plot(M)
   end

mertens_plot

Postscript

I started this project by being surprised to find myself computing determinants. Now I am back to my long-time position disparaging determinants. They have been replaced by a good friend, backslash.

Get the MATLAB code

Published with MATLAB® R2024a