How Long Is a Winter’s Day?
Happy December! The days sure seem longer in the winter. Of course, there are fewer hours of daylight. But the actual span of the day seems longer. Or is that just a psychological effect? Let’s investigate!
How long is a day?
The first answer that jumps into your head is probably 24 hours. But that just leads to my next question. How long is an hour? If the first answer that jumps into your head 1/24 of a day, then you can see that there’s something circular going on.
If you think about it a little longer, you’re likely to come up with something like this. A day is the amount of time between one day and the next. But as measured by what? As modern folk, we tend to start with well-defined seconds and build up from there. One day equals 60 x 60 x 24 = 86,400 seconds. But seconds must have originally been defined in the other direction, starting with days. At this point, it helps to think like an Old One. How did the ancient Egyptians, for example, measure a day?
We can measure the sun’s progress through the sky with a sundial. Noon happens when the shadow from a sundial gnomon (the pointy bit) stops getting shorter and starts getting longer. This is called “local noon” to distinguish it from the noon you see on a clock. So one day is the time it takes from local noon on one day until local noon the next day. We can use MATLAB to illustrate this. I will use the file sunshadow.m written by (ahem) yours truly, although the algorithms I used come from De Zonnewijzerkring (the Netherlands Sundial Society). I, for one, am glad to live in a world that contains a Netherlands Sundial Society.
Here’s an animation.

Every day the sun takes a slightly different path through the sky. So the path of the shadow along the ground is going to be different too.
Shown below is the gnomon’s shadow path for December 8, 2020 at my latitude, 42.3 degrees north. For reference, I’m also showing the shadow for a summer day, six months later. You’re looking straight down on a stick (gnomon) that is one meter long. North is in the positive y direction.
lat = 42.3; d = day(datetime(2020,12,8),"dayofyear"); [x,y] = sunshadow(lat,d,linspace(8.05,15.7,100)); plot(x,y,'LineWidth',2) hold on d = day(datetime(2021,6,8),"dayofyear"); [x,y] = sunshadow(lat,d,linspace(5.2,18.75,100)); plot(x,y,'LineWidth',2) line(0,0,'LineStyle','none','Marker','.','MarkerSize',24,'Color',[0 0 0]) hold off axis equal grid on title('Sundial Shadows in Winter and Summer') legend({'shadow in December','shadow in June','gnomon'}, ... "Location","south")

From this diagram we can see that, in the winter (in the northern hemisphere) the sun sets south of west (so the shadow points north), and in the summer the situation is reversed.
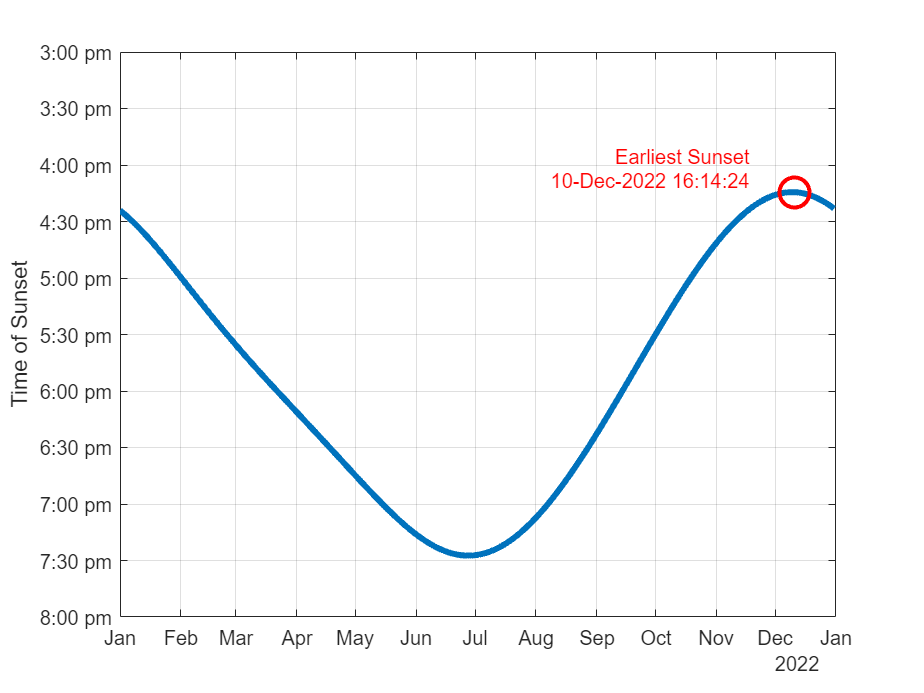
Now, if we accurately measure the time from noon to noon, we can get a sense for exactly how long the day is. I’m using another offering from the File Exchange to calculate sunrise, local noon, and sunset. This is SUNRISE from François Beauducel.
lat = 42.3; lon = -71.3; alt = 0; tzone = -5; d = datetime(2020,7,1:365); [srise,sset,noon] = sunrise(lat,lon,alt,tzone,datenum(d)); sriseHour = 24*(srise - floor(srise)); ssetHour = 24*(sset - floor(sset)); localNoonHour = 24*(noon - floor(noon)); plot(d,sriseHour,'LineWidth',2) hold on plot(d,ssetHour,'LineWidth',2) plot(d,localNoonHour,'LineWidth',2) hold off dc = datetime(2020,12,8); xline(dc,'Color','red'); grid on ylabel('Hour of the Day') legend({'sunrise','sunset','local noon','8 December'})

I’m showing sunrise and sunset here, but I’m most interested in the wiggly yellow line in the middle. Local noon is a wiggly line! What’s up with that?
Let’s zoom in. At my latitude, this is when the sun is right overhead.
plot(d,localNoonHour,'.') grid on yt = linspace(11,12,13); ytl = strings(size(yt)); for i = 1:length(yt) ytl(i) = sprintf("%2d:%02d", ... floor(yt(i)), ... round((yt(i) - floor(yt(i)))*60)); end set(gca,'YTick',yt,'YTickLabel',ytl) ylabel('Time of Day') title('Time of Local Noon')

But this is all building up to the big question. What we REALLY want to know is: how long is it from one noon to the next? That’s the prize, the true length of a day.
dayLength = (diff(noon)*24 - 24)*60*60; plot(d(2:end),dayLength,'.') grid on title('Deviation from 24 Hour Day in Seconds') ylabel('Deviation (sec)')

And there you have it. The length of a day varies by around 50 seconds depending on the time of year. There are only a few days every year that are exactly 24 hours long. And although it’s well known that daylight hours change depending on your latitude, this varying day length is constant. It’s the same all over the world.
We haven’t talked about why this is true, and sadly I’ve run completely out of pixels for today’s post. But Wikipedia’s Equation of Time article does a good job explaining why you can blame it on two weird things about Earth. First, Earth’s orbit is an ellipse, not a circle. And second, the Earth is tilted on its axis.
But we have answered our big question for the day. The days are truly and literally longer in the winter… if your winter includes December. A more complete statement is that the days are genuinely longer in December all around the world, regardless of the season. But only if you define day as local noon to local noon. Which nobody really does, since we use an annualized mean solar time to keep from going insane.
But true solar time is more fun.
The end.








댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.