Like millions of other folks, I play Wordle from the New York Times almost every day. The Times reports that Wordle puzzle number 1497 on Friday, July 25, was especially difficult. The average puzzler required 5.7 attempts and many failed to get the answer in the six moves allowed. I have a MATLAB assistant that I call Wordler and, even with her help, I failed on number 1497. Here's why.... 더 읽어보기 >>

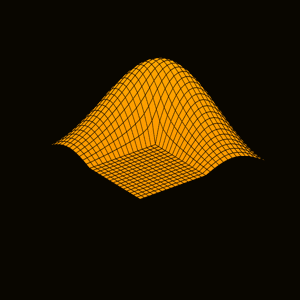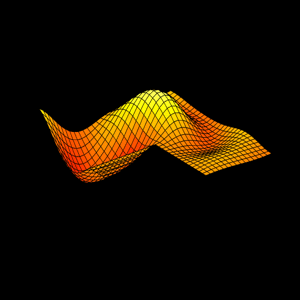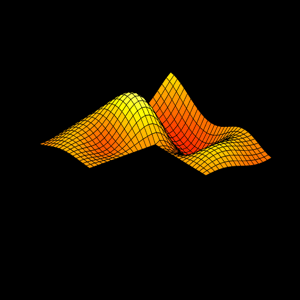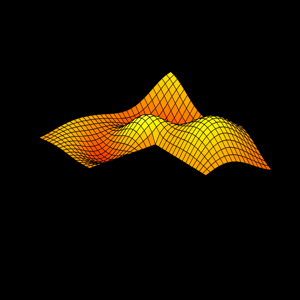
In 1988, while I was with Ardent Computer in Silicon Valley, I gave a talk that previewed MATLAB graphics. The title was "Pictures of Matrices". At the time, a mathematician friend of mine asked.... 더 읽어보기 >>

The twenty-second Householder Symposium on Numerical Linear Algebra was held June 8 - June 13 at Cornell. The local organizers were Anil Damle, Alex Townsend and David Bindel. Anil served as host and cheerleader.... 더 읽어보기 >>

The twenty-second Householder Symposium on Numerical Linear Algebra is this week, June 8 - June 13, 2025 at Cornell. My talk on Wednesday had the provocative title "A Million-Dollar Matrix". A PDF of the slides available at link_1. The talk covers posts in the Cleve's Corner blog last fall. link_2, link_3, link_4.... 더 읽어보기 >>

The Revolving Century puzzle is a beautifully made wooden puzzle from Creative Crafthouse in Hudson, Florida.... 더 읽어보기 >>

No, this is not the script for an episode of "Game of Thrones". It is a blog post about Lindenmayer grammars, growing plants, space-filling fractals, turtle graphics and dragon curves.... 더 읽어보기 >>

Two years ago, in March of 2023, an unlikely team of mathematical hobbyists announced the discovery of a remarkable 13-sided polygon that they nick-named the "Hat". Today, a Google search for the Hat's more formal name, "Aperiodic Monotile", yields dozens of links.... 더 읽어보기 >>

A look at the structure, and the eigenvalues and singular values of interesting test matrices.... 더 읽어보기 >>

MATLAB has two different ways to compute singular values. The easiest is to compute the singular values without the singular vectors. Use svd with one output argument, s1.... 더 읽어보기 >>

LUTool provides an interactive animation of Gaussian elimination, the most important algorithm in technical computing.... 더 읽어보기 >>