Keeling Spiral
The Keeling Spiral
Today we're going to take a look at what is probably the most famous dataset in atmospheric science, the Keeling Curve. This is a timeseries dataset of the concentration of carbon dioxide at an observatory on Mauna Loa. Charles Keeling started collecting this data in 1974. It's available online at the following URL.
s = urlread('ftp://aftp.cmdl.noaa.gov/products/trends/co2/co2_weekly_mlo.txt'); c = strsplit(s,'\n');
The file is a pretty simple text format. We just need to break it into individual lines and pull out the fields we want. We want the date (which is stored in the first 3 columns) and the "CO2 molfrac" which is stored in the 5th column.
nl = length(c); dates = datetime.empty; molfrac = []; for i=1:nl % Comment lines start with # if isempty(c{i}) || c{i}(1) == '#' continue end % Get all the fields lab = strsplit(c{i}); value_str = lab{6}; dates(end+1) = datetime(str2double(lab{2}), ... str2double(lab{3}), ... str2double(lab{4})); % -999.99 means missing data if strcmp(value_str,'-999.99') molfrac(end+1) = nan; else molfrac(end+1) = str2double(value_str); end end
At this point, we have two arrays. * dates is an array of datetime values when the measurements were taken. * molfrac is a numeric array with the measurements in parts per million.
Lets start out with a simple plot.
plot(dates,molfrac) xlabel('Date') ylabel('parts per million') title('Atmospheric CO_2 at Mauna Loa');
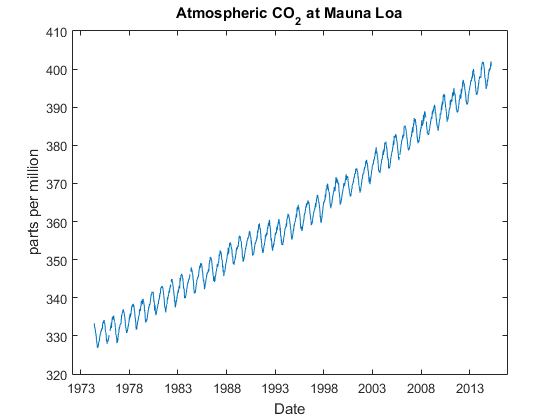
As you can see, the CO2 level keeps going up every year, but it also bounces up and down quite a bit. That's because there's a seasonal variation in the level of CO2 that's related to things like the rate at which plants are growing. We can see this if we zoom in on a single year.
mask = year(dates)==1987;
plot(dates(mask),molfrac(mask))
title('Atmospheric CO_2 at Mauna Loa, 1987');

One simple way to deal with this seasonality is to break the dataset into individual years, and plot them all together. We do this by looping over the years, pulling out the values where "year(dates)" matches our loop index, and then computing the number of days since January 1st of that year.
cla reset hold on for yidx=1974:2015 mask = year(dates)==yidx; plot(days(dates(mask)-datetime(yidx,1,1)),molfrac(mask)); end xlim([0 365]) xlabel('Day of Year') ylabel('parts per million') title('Atmospheric CO_2 at Mauna Loa');

But we really need to improve the tick labels with this view. We can use the datestr function to get a nicer label for the days.
xlabel('') ax = gca; x = ax.XTick; lab = cell(size(x)); for i=1:length(x) lab{i} = datestr(datetime(2015,1,1) + days(x(i)), 'mmm dd'); end ax.XTickLabel = lab; ax.XTickLabelRotation = 45;

Stacking 2D lines shows us how the CO2 level moves up each year, but what would it look like if we plotted it in 3D? That's pretty easily done by creating an array of years and an array of "day of the year".
yr = zeros(size(molfrac)); dofy = zeros(size(molfrac)); for yidx=1974:2015 mask = year(dates) == yidx; yr(mask) = yidx; dofy(mask) = days(dates(mask) - datetime(yidx,1,1)); end hold off cla reset for yidx=1974:2015 mask = year(dates) == yidx; line(dofy(mask), yr(mask), molfrac(mask)); end box on grid on view(3) xlim([0 365]) ylim([1974 2015])

And again, we'll want to pretty up the labels.
ax = gca; x = ax.XTick; lab = cell(size(x)); for i=1:length(x) lab{i} = datestr(datetime(2015,1,1) + days(x(i)), 'mmm dd'); end ax.XTickLabel = lab; xlabel('Day') ylabel('Year') zlabel('parts per million') title('Atmospheric CO_2 at Mauna Loa');

We could also use scatter3 to plot molfrac against the yr and dofy arrays. That gives us something that looks a little like a surface.
scatter3(dofy,yr,molfrac) xlim([0 365]) ylim([1974 2015])

But it'd be nice if that really was a surface plot. We can't use the surface command because this isn't a regular grid. We could pad the first year and last year out to 52 weeks by adding nans, but there are also years that have 53 weeks, such as 1978.
We can skip the gridding problem by using trisurf, but that means we'll need to triangulate the data. Lets try using Delaunay triangulation. BTW, the divide by 7 is required because Delaunay triangulation works best when the X & Y scaling is close to uniform.
tri = delaunay(yr,dofy/7);
h = trisurf(tri,dofy,yr,molfrac);
h.EdgeColor = 'none';
h.SpecularStrength = .25;
ylim([1974 2015])
camlight

That looks pretty interesting. We can now rotate it around and see some details about how the different years relate to each other. But as you can see there is something funny going on at the edges. If we look straight down and zoom in, we can figure out what's happening:
xlim([0 200]) ylim([1970 1980]) h.FaceLighting = 'none'; h.EdgeColor = 'black'; view(2)

The call to delaunay created triangles between the first day (19-May-1974) and lots of different days in 1975. The Delaunay triangulation includes these triangles because they're part of the convex hull of the points, but they're not really meaningful for our purposes. We can get rid of those by walking through the array of triangles and throwing away any with long edges.
max_x = 1; max_y = 15; long_x = (abs(yr(tri(:,1))-yr(tri(:,2))) > max_x) ... | (abs(yr(tri(:,2))-yr(tri(:,3))) > max_x) ... | (abs(yr(tri(:,3))-yr(tri(:,1))) > max_x); long_y = (abs(dofy(tri(:,1))-dofy(tri(:,2))) > max_y) ... | (abs(dofy(tri(:,2))-dofy(tri(:,3))) > max_y) ... | (abs(dofy(tri(:,3))-dofy(tri(:,1))) > max_y); tri = tri(~(long_x | long_y),:); h = trisurf(tri,dofy,yr,molfrac); h.EdgeColor = 'none'; h.SpecularStrength = .25; camlight view(2)

Now we'll go back to our 3D view.
view(3) xlim([0 365]) ylim([1974 2015]) zlim([-inf inf]) ax = gca; t = ax.XTick; lab = cell(size(t)); for i=1:length(t) lab{i} = datestr(datetime(2015,1,1) + days(t(i)), 'mmm dd'); end ax.XTickLabel = lab; xlabel('Day') ylabel('Year') zlabel('parts per million') box on

But there's a problem with this visualization. The last day of one year is actually adjacent to the first day of the next year, but in this visualization they're on opposite sides of the chart. What if we rolled this around a cylinder? We'll make a cylindrical chart where the angle is the day of the year, the Z is the year, and the radius is the measurement of the CO2 level.
[x,y,z] = pol2cart(2*pi*dofy/365, molfrac, yr+dofy/365); h = trisurf(tri,x,y,z); h.FaceVertexCData = molfrac'; h.FaceColor = 'interp'; h.SpecularStrength = .25; line([0 0],[0 0],[1970 2020],'Color',[.75 .75 .75],'LineWidth',3) camlight xlim([-405 405]) ylim([-405 405]) zlim([1974 2015])

That's kind of interesting, but we can see that there's a rip down the back. That's because the Delaunay triangulation didn't know that those samples were near each other. It was working in a 2D plane which had a cut rather than in the cyclic surface of the cylinder. We'll need to do our own triangulation. This can be kind of tedious, so I'll just pull out one I prepared earlier like Julia Child used to do on her TV show. You can download it here.
tri = stripyears(yr,dofy); [x,y,z] = pol2cart(2*pi*dofy/365, molfrac, yr+dofy/365); h = trisurf(tri,x,y,z); h.FaceVertexCData = molfrac'; h.FaceColor = 'interp'; h.SpecularStrength = .25; line([0 0],[0 0],[1970 2020],'Color',[.75 .75 .75],'LineWidth',3) light('Position',[-1 -.5 -.25]); light('Position',[-1.5 .5 .25]); xlim([-405 405]) ylim([-405 405]) zlim([1974 2015])

This results in a fairly unusual visualization that I saw used a few times back in the 80's, but I don't think that it's been used much since. That was really the dawn of 3D in data visualization, so we were probably just getting carried away with our new toy. It certainly has some limitations. But lets see if there's anything we can do to make it more useful.
The first thing we should do is fix the datatips so that they display the date and value from the dataset, rather than the X, Y, & Z coordinates. That's actually pretty easy. We just need this simple function:
type keeling_datatip.m dcm = datacursormode(gcf); dcm.Enable = 'on'; dcm.UpdateFcn = @keeling_datatip;
function txt = keeling_datatip(~,evd)
[th,r,z] = cart2pol(evd.Position(1),evd.Position(2),evd.Position(3));
th = mod(th,2*pi);
d = datetime(floor(z),1,1) + days(365*th/(2*pi));
txt = {['Date: ', datestr(d)], ...
['Value: ', num2str(r,4)]};
end

Another thing we can do is to exagerate the radius. That will make the variations in the radius more visible. We could also get rid of the edges and switch to Gouraud lighting.
roffset = 300; [x,y,z] = pol2cart(2*pi*dofy/365, molfrac-roffset, yr+dofy/365); h = trisurf(tri,x,y,z); h.FaceVertexCData = molfrac'; h.FaceColor = 'interp'; h.EdgeColor = 'none'; h.FaceLighting = 'gouraud'; h.SpecularStrength = .25; line([0 0],[0 0],[1970 2020],'Color',[.75 .75 .75],'LineWidth',3) l1 = light('Position',[-1 -.5 -.25]); l2 = light('Position',[-1.5 .5 .25]); xlim([-105 105]) ylim([-105 105]) zlim([1974 2015])

But when with the new radius scale, we need to fix the X & Y ticks to account for the offset.
ax = gca; t = ax.XTick; lab = cell(size(t)); for i=1:length(t) lab{i} = num2str(abs(t(i))+roffset); end ax.XTickLabel = lab; ax.YTick = t; ax.YTickLabel = lab; xlabel('parts per million') ylabel('parts per million') zlabel('Year') title('Atmospheric CO_2 at Mauna Loa');

What do you think? Can you think of cases where this visualization might be useful? Can you think of any additional tweaks which might make it more useful?
- 범주:
- Charts


