Generating Hilbert curves
This week I came across some files I wrote about 16 years ago to compute Hilbert curves. A Hilbert curve is a type of fractal curve; here is a sample:

I can't remember why I was working on this. Possibly I was anticipating that 16 years in the future, during an unusually mild New England winter, I would be looking for a blog topic.
Anyway, there are several interesting ways to code up a Hilbert curve generator. My old code for generating the Hilbert curve followed the J. G. Griffiths, "Table-driven Algorithms for Generating Space-Filling Curves," Computer-Aided Design, v.17, pp. 37-41, 1985. Here's the basic procedure:
First, initialize four curves, \( A_0 \), \( B_0 \), \( C_0 \), and \( D_0 \), to be empty (no points).
Then, build up the Hilbert curve iteratively as follows:
\[ A_{n+1} = [B_n, N, A_n, E, A_n, S, C_n] \]
\[ B_{n+1} = [A_n, E, B_n, N, B_n, W, D_n] \]
\[ C_{n+1} = [D_n, W, C_n, S, C_n, E, A_n] \]
\[ D_{n+1} = [C_n, S, D_n, W, D_n, N, B_n] \]
where \( N \) represents a unit step up, \( E \) is a unit step to the right, \( S \), is a unit step down, and \( W \) is a unit step left.
One way to code this procedure is to incrementally build up a set of vectors that define the step from one point on the path to the next, and then to use a cumulative summation at the end to turn the steps into x-y coordinates. Here's how you might do it.
A = zeros(0,2); B = zeros(0,2); C = zeros(0,2); D = zeros(0,2); north = [ 0 1]; east = [ 1 0]; south = [ 0 -1]; west = [-1 0]; order = 3; for n = 1:order AA = [B ; north ; A ; east ; A ; south ; C]; BB = [A ; east ; B ; north ; B ; west ; D]; CC = [D ; west ; C ; south ; C ; east ; A]; DD = [C ; south ; D ; west ; D ; north ; B]; A = AA; B = BB; C = CC; D = DD; end A = [0 0; cumsum(A)]; plot(A(:,1), A(:,2), 'clipping', 'off') axis equal, axis off

I was curious to see what might be on the MATLAB Central File Exchange, so I searched for "hilbert curve" and found several interesting contributions. There are a couple of 3-D Hilbert curve generators, and several different ways of coding up a 2-D Hilbert curve generator. I was particularly interested in the Fractal Curves contribution by Jonas Lundgren.
Jonas shows a much more compact implementation of the ideas above using complex arithmetic. It looks like this:
a = 1 + 1i; b = 1 - 1i; % Generate point sequence z = 0; order = 5; for k = 1:order w = 1i*conj(z); z = [w-a; z-b; z+a; b-w]/2; end plot(z, 'clipping', 'off') axis equal, axis off

Jonas' contribution includes several other curve generators. Here's one called "dragon".
z = dragon(12);
plot(z), axis equal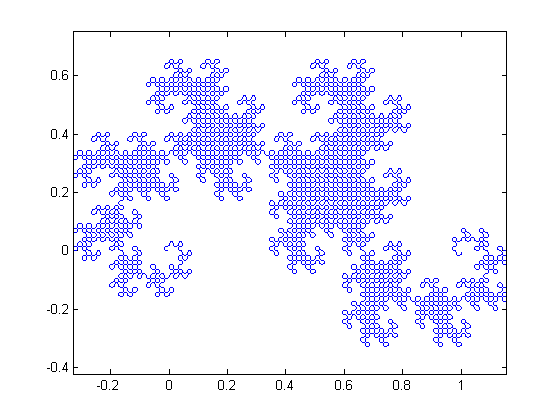
Here's a zoom-in view of a portion of the dragon.
axis([-.1 0.2 0.4 0.7])
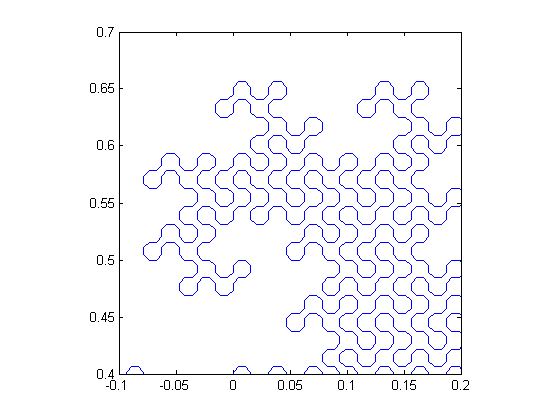
What do you think? Does anyone know of an image processing application for shape-filling curves? Please leave a comment.









评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。