Polygons, Polyshapes and Puzzles
Until recently, I knew nothing about the polyshape object in MATLAB. Now I can use polyshape to simulate an extraordinary puzzle.
Contents
Puzzles
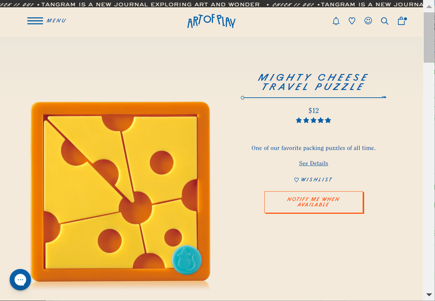
The Web site Art of Play, from some folks in San Diego, has well over two-hundred puzzles. Recently, one of their most popular puzzles, Mighty Cheese, caught my attention. The idea is to move the slices of plastic cheese around within the frame in order to create a hole large enough to hold the little plastic mouse. However, when I last checked, Mighty Cheese was sold out. Not wanting to be dissuaded by the unavailability of the puzzle itself, and not knowing the solution, I set out to build a simulator.
Not a T
I expected Mighty Cheese to be something like the T-puzzle that I enjoyed several years ago. But, unlike the T, the geometry of cheese cannot be modelled by simple rectangular patches. I needed help. Steve Eddins answered my plea and told me about MATLAB's "polyshapes". That led to this blog post.
A slice of cheese
A "selfie" of a cheese slice provides an example of a polyshape. It has curved boundaries and a hole. The MATLAB documentation for polyshape says this a polygon. In my mathematical world, polygons can't have curved boundaries or holes. But, I guess that I am being pedantic.

I began with this photo of the Mighty Cheese puzzle.
puzzle = imread('Cheese_puzzle.png');

Two lines of code and the L*a*b color model find the regions in photo that look like cheese.
[L,a,b] = imsplit(rgb2lab(puzzle)); mask = a > 30; spy(mask)
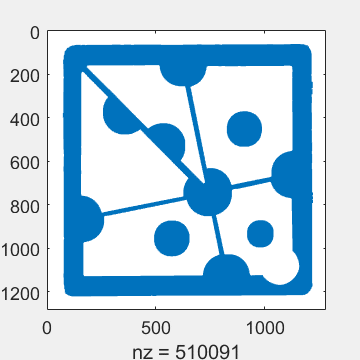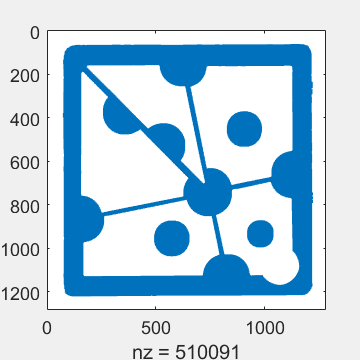
Steve provided a function that turns mask into a polyshape object.
slice = my_polyshapes(mask);
An overloaded plot function then generates the selfie from slice.
sliceplot = plot(slice, ... 'facecolor',cheese_yellow, ... 'facealpha',1);
My first solution
I didn't use AI or simulated annealing or any other modern technique to search for a solution. I just poked around while I was learning about polyshapes and programming my simulator. It was just me and a real mouse. No, not a real real mouse. You know the kind I mean.

Is this solution correct?
I almost made a blog post claiming this is the solution the designers of Mighty Cheese must have had in mind. But I wasn't sure. My solution made use of the white space around the outside edges of the slices. How wide are those gaps? I didn't yet have a real physical puzzle to measure tolerances.
Spoiler alert !
I am sure glad now that I didn't post that "solution". It wasn't correct, and it wasn't pretty.
This puzzle is not as easy as it looks. In fact, the solution is very hard to find and is very elegant. If you want to try to solve it yourself, stop reading this post, bookmark this spot, and come back later.
My second solution
As I should have known, this puzzle is no secret to the Internet It is available for about $10 at many places and YouTube offers several solutions. But I'm glad that I didn't see any of them until a few weeks ago.
When I made more careful measurements on "Cheese_puzzle.png" and had a more accurate model to simulate, it became clear that my precious first solution just wouldn't fit.
A round peg in a square hole
Nobody said that the mouse had to fit neatly into a circular hole with just the right diameter. Once you realize that you might be looking for a noncircular hole, you are on the way to finding the solution.
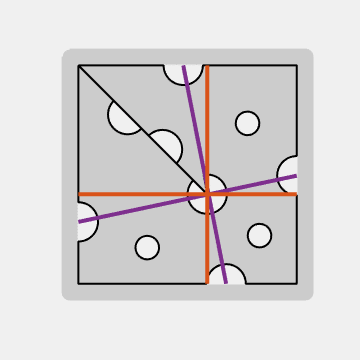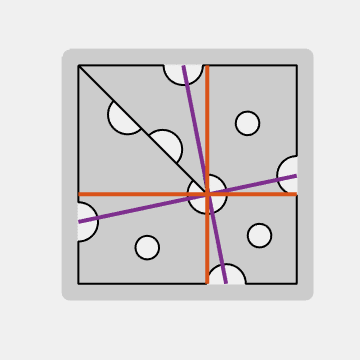
Theta
The key to the puzzle's geometry is the purple axes in this picture. They cross at right angles at a point in the center hole at the tip of the protruding slice. The angle between the purple axes and the orange vertical/horizontal axes can be measured accurately on the photo and everything else follows. The angle is
theta = atand((y(b)-y(a))/(b-a)) = 11.62 degrees
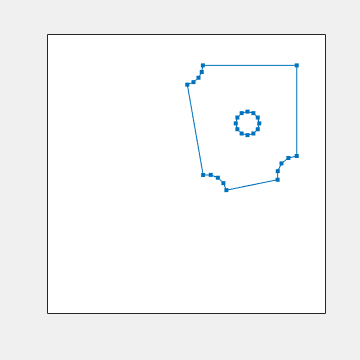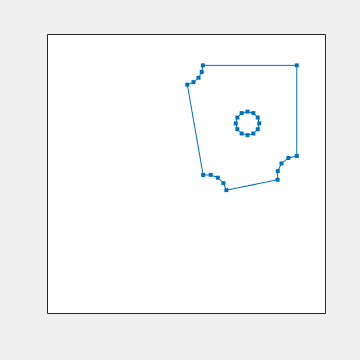
Polyshapes
The mask that I was using for my first solution got me started with polyshapes, but I eventually abandoned it. It is easy to make a polyshape directly from a list of points around the boundary, like this.
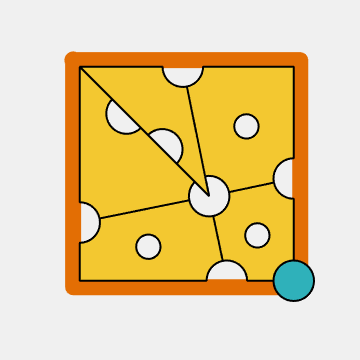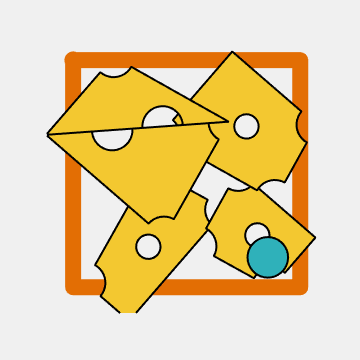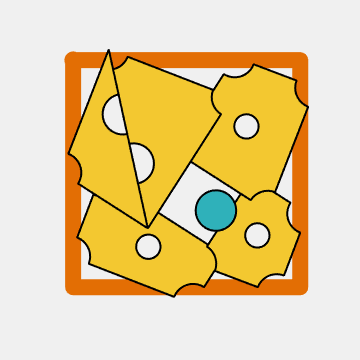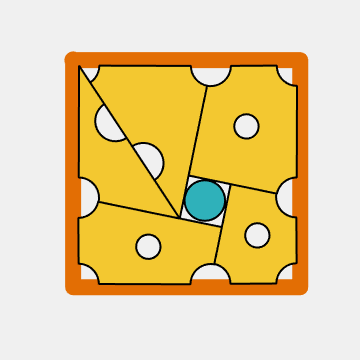
The solution
The three holes in the original cheese slices do not appear to serve any purpose. So, I have moved them and given them an important role in this simulation. Combine the two triangular slices in the upper left into a single slice. Rotate each of the resulting four slices by an angle of 180-theta = 168.38 degrees about its center. The four right-angled corners from the central hole go to the corners of the puzzle while the outer corners form a central square just large enough to hold the mouse.
That is really elegant.
Where did this puzzle originate? What mathematics was involved in its design?
Software
My code is here: Mighty_Polyshape.m.







评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。