Solving Higher-Order ODEs in MATLAB
In a comment to last year's introduction to the new ODE solution framework in MATLAB, Ron asked if I could provide an example of using it to solve a 2nd order ODE since most tutorials don't deal with the new syntax. Absolutely I can!
So let's start at the beginning. An ordinary differential equation (ODE) contains one or more derivatives of a dependent variable, y, with respect to a single independent variable, t, usually referred to as time. The notation used here for representing derivatives of y with respect to t is y′ for a first derivative, y′′ for a second derivative, and so on. The order of the ODE is equal to the highest-order derivative of y that appears in the equation.
This equation then is second order
MATLAB's current crop of numerical ODE solvers only solve first order equations so we have work to do before we can proceed. It turns out that you can write any higher-order ODE as a system of first-order ODEs.
Calculating the system of ODEs by hand
You first make the following definitions
Then we take their derivatives
Do substitutions using our definitions and our original second order equation
and we have our system of first order ODEs. We write this system as the following function
% Define the system of first-order ODEs
k = 10; % Spring Constant
m = 1; % Mass
odeSystem = @(t, y) [y(2); -k/m * y(1)];
So far, nothing is new. This is the exact same method you've always had to follow for doing this in MATLAB.
We plug odeSystem into the new framework as follows, also stating our initial conditions which are y=1 and y'=0 at t=0. This is the only step that's different from any tutorials you might have seen before.
shm = ode(ODEFcn=odeSystem,InitialTime=0,InitialValue=[1;0]);
shmSol = solve(shm,-5,5);
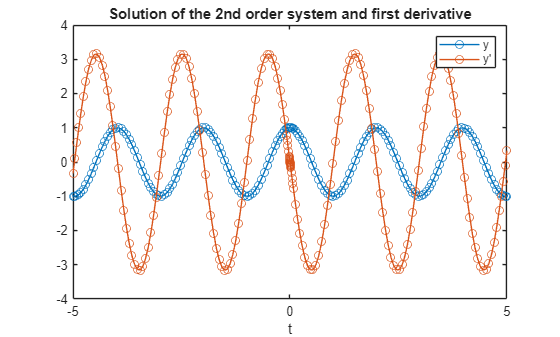
plot(shmSol.Time,shmSol.Solution,'-o');
legend(["y","y'"])
title("Solution of the 2nd order system and first derivative")
xlabel("t")
Making use of a solutionFcn
Something to point out here is that our starting point is at t=0 and that since we asked for a range from t=-5 to t=5 we are integrating in both directions automatically, allowing the solver to chose whatever values of t it deems are best. As you can see from the plot above, the solver used a lot of points around t=0 in both directions.
We can get more control by defining a solutionFcn. Then we can see the solution at a set of uniform points in time
y = solutionFcn(shm,-5,5,OutputVariables=1); % Represents the solution of our system
t = linspace(-5,5,100);
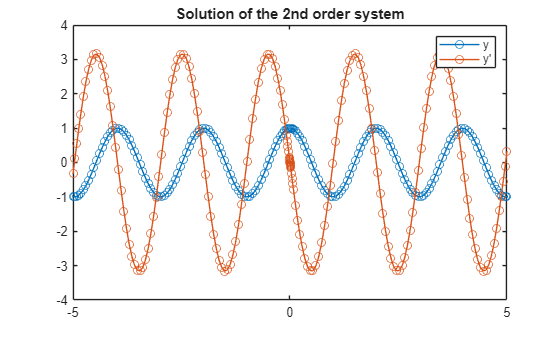
plot(t,y(t),'-o')
title("Solution of the 2nd order system")
xlabel("t")
To recover the derivative, use the second output of the solutionFcn, y
[yt,ypt] = y(t);
plot(t,yt,'-o',t,ypt,'-o')
legend(["y","y'"])
title("Solution of the 2nd order system and first derivative")
xlabel("t")
Calculating the system of ODEs using Symbolic Toolbox
I'm not going to lie to you, I don't trust it when I do mathematics by hand. Even for something as simple as this I make mistakes and for a more complex equation you can bet good money that I'll mess it up. I much prefer it when I can get the computer to do the heavy lifting for me. That's what they are for!
I started off by asking development why we don't 'just' support higher order ODEs directly in the new framework. Once I put my dollar in the 'Just Jar', they told me that its something they've thought about off and on for a while. Could I get more user stories where people would value such functionality? So here I am asking, dear reader, would such direct support be useful for you and, if so, what's your application?
In the meantime, I found a page in the documentation that shows how to use symbolic toolbox to do the transformation to a system of ODEs for us using the odeToVectorField function. Let's apply it to the problem here. Recall, this is the problem we want to solve
We set up some symbolic variables
syms y(t) m k
and pass our equation to odeToVectorField using the Symbolic Toolbox function diff to handle the derivatives
[V] = odeToVectorField(m*diff(y, 2) + k*y ==0)
That result looks familiar! It's the same system I derived by hand earlier. We need to convert it to a MATLAB function so I can pass it to the numerical ODE framework
M = matlabFunction(V,'vars',{'t','Y','m','k'})
Now I need to sort out the parameters m and k. The function above has four input parameters but I want one that only takes two.
k = 10; % Spring Constant
m = 1; % Mass
odeSystemFromSymbolic = @(t, y) M(t,y,m,k)
we pass this into the ODE framework as before
shm = ode(ODEFcn=odeSystemFromSymbolic,InitialTime=0,InitialValue=[1;0]);
shmSol = solve(shm,-5,5);
plot(shmSol.Time,shmSol.Solution,'-o');
legend(["y","y'"])
title("Solution of the 2nd order system")
This gives the identical result but I didn't need to any algebra by hand, which is always a good thing! Of course, we are also free to use any of the other machinery in the new ODE framework including solutionFcn but I won't show that again for the sake of space.



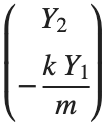








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.