How to run local DeepSeek models and use them with MATLAB
Almost immediately after the DeepSeek-R1 AI models were made available to the world, people started asking how you can use them in MATLAB. Late last week, Vasileios Papanastasiou, a software test engineer at MathWorks, posted how to do this on LinkedIn and this morning I tried out his instructions for the first time on my own machine.
Running deepseek-r1:1.5b on my local machine
I am going to make use of the "Large Language Models (LLMS) with MATLAB" add-on along with ollama to run one of the smaller deepseek models on my local machine and interact with it in MATLAB. Following Vasileios's instructions, the first thing I did was
Download and install Ollama: https://ollama.com/download
I did this on Windows. As soon as the installation was complete, I opened up an operating system command line and ran the command
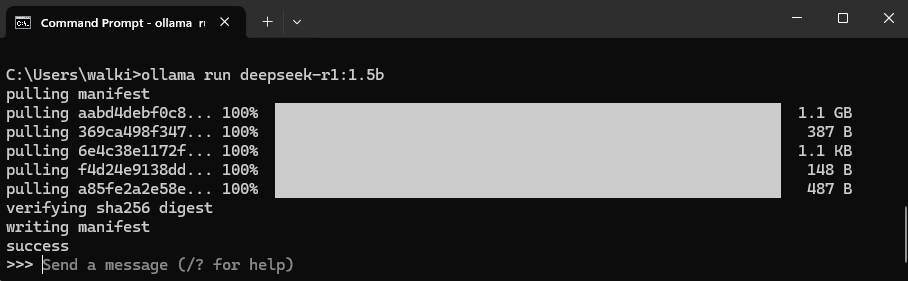
ollama run deepseek-r1:1.5b
This installs a 1.5 billion parameter model, which is pretty small but hopefully means that I don't need to worry about computational resource constraints. I can always try larger models later.
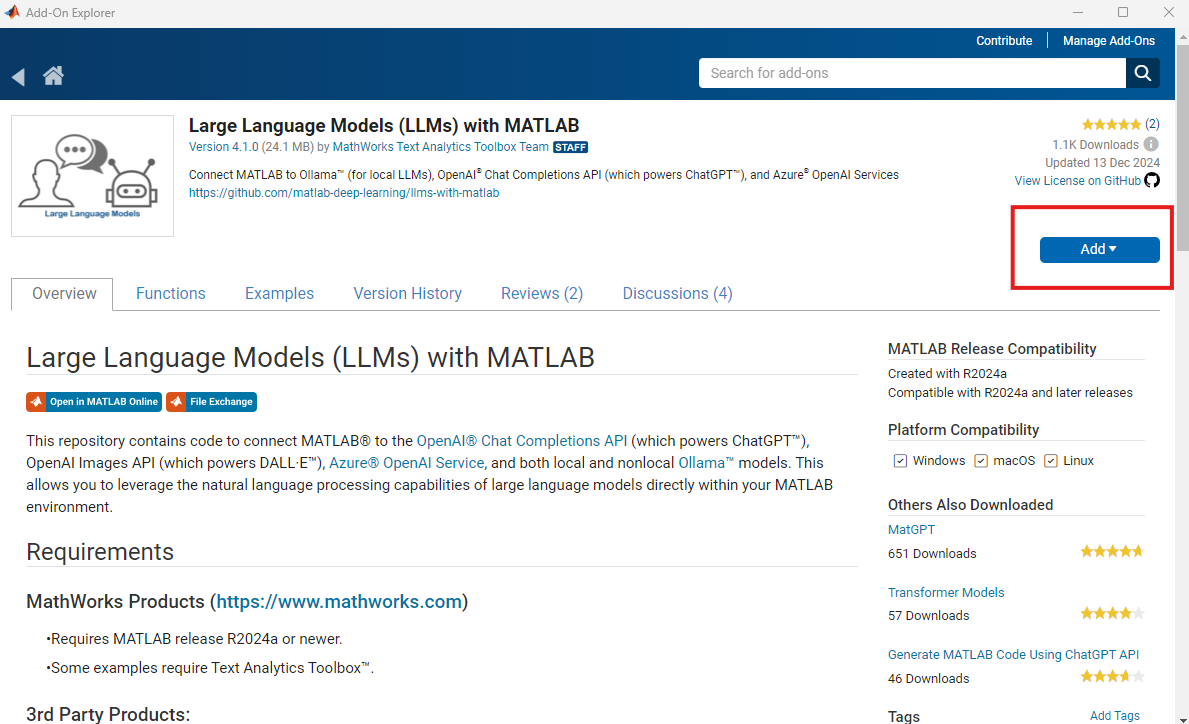
Now, over to MATLAB. Vasileios suggested that we get the "Large Language Models (LLMS) with MATLAB" add-on from GitHub but I took a different route. I clicked on Add-ons in the Environment tab of MATLAB R2024b

From the Add-on explorer, I searched for 'Large Language Models' and when I found it clicked on 'Add'. This took care of download and installation.
That takes care of installation. Let's start playing with it in MATLAB. First, let's create an ollamaChat object
chat = ollamaChat("deepseek-r1:1.5b")
chat =
ollamaChat with properties:
ModelName: "deepseek-r1:1.5b"
Endpoint: "127.0.0.1:11434"
TopK: Inf
MinP: 0
TailFreeSamplingZ: 1
Temperature: 1
TopP: 1
StopSequences: [0×0 string]
TimeOut: 120
SystemPrompt: []
ResponseFormat: "text"
Finally, we can try talking to the AI
txt = generate(chat,"What is the speed of light?")
txt =
"<think>
</think>
The exact value of the speed of light in a vacuum is defined as \( 299,792,458 \) meters per second.
This precise definition ensures consistency and accuracy across all scientific measurements and calculations."
Something I find fun about LLM models like this is that you can ask the same question over and over again and get a different answer each time which reflects the stochastic nature of them. Sometimes the result is just a little different
txt = generate(chat,"What is the speed of light?")
txt =
"<think>
</think>
The speed of light in a vacuum is approximately 299,792 kilometers (186,282 statute miles) per second.
Light is the fastest thing in the universe with its universal speed limit."
and other times it is very wordy indeed with a lot of 'thinking'.
txt = generate(chat,"What is the speed of light?")
txt =
"<think>
Okay, so I'm trying to figure out what the speed of light is. I've heard it's something really important in physics,
especially with relativity and electromagnetism.
Let me see... I remember that it's called c, but exactly how much is it?
First, I think about units. The speed should be in meters per second because [there's a big unit for that out there. ' ...
Maybe like 3 times something—maybe 299 million something? Oh, yeah, the original value was 299,792,458 meters per second.
That seems familiar. Wait, isn't that what it is now?
But I should check if this number makes sense. Why is it so high compared to the speed of trains or planes?
Because light is such a fast thing, traveling through space at around 300 million meters each second
—it's way faster than anything else on Earth.
I also recall units in different systems. [It's not just SI, am I right? Maybe another one.
Wait, in cgs units, which are centimeters and grams, the speed would probably be something times a billion or so cm per second.
But that seems less relevant now.
Now, how was this value first determined? I think it came out of [Maxwell's equations when considering the speed at which
electric and magnetic fields propagate through space without any medium—so in a vacuum.
That must have been quite a theoretical push by scientists.
Einstein later connected this to special relativity when he needed a way for electrons to accelerate without contradictions.
In everyday terms, c tells us how quickly signals like light or radio waves can move across the universe.
Without it being so fast, life would be very different, especially in astronomy where such vast distances are covered quickly.
It's like something almost instantaneous but still moving at a significant pace due to its high value.
But wait, is there any way it could change? Is it constant or does light slow down in some circumstances?
I haven't heard of the speed of light changing so far.
Maybe in extreme conditions, like near superconductors or high temperatures, materials might influence [vacuum']s properties,
affecting how light travels through them.
But most physicists today would say c is a fundamental, unchanging constant.
I also remember that special relativity deals with how different observers measure time and space when they move relative to each other.
Light speed being invariant means all observers agree on its value regardless of their motion relative to the light,
which helps unify space and time into spacetime.
So putting it all together: c is 299,792,458 meters per second precisely—I should check if that's accurate.
Maybe I've heard it rounded up or kept more decimal places.
Oh yeah, sometimes calculations round it to about 300 million m/s for simplicity, but the correct value has all those digits.
I think c is crucial in so many areas like time dilation and the structure of space-time from general relativity.
It's the cornerstone we use to solve problems in physics whenever a high-speed scenario comes into play without any medium
to slow things down. Without it being that fast, it wouldn't be as impactful or as something we can use in equations.
So just recapitulating: The speed of light is approximately three times 10^8 meters per second but precisely calculated to around
299,792,458 m/s. That's why things moving at that speed sound so rapid compared to everyday experiences.
It's a constant that underpins the fabric of spacetime and has far-reaching implications in both theoretical physics and applied fields.
</think>
The speed of light is approximately **299,792,458 meters per second**, symbolized by the letter c.
This is a fundamental constant in physics, unchanging at 299,792,458 m/s exactly today.
The unit "m·s−¹" indicates meters per second.
The value of c was determined theoretically as electromagnetic waves travel through a vacuum, where electric and
magnetic fields propagate instantaneously without needing any medium.
It's crucial in special relativity because it serves as an invariant, meaning all observers agree on its speed
irrespective of their relative motion. In high-speed scenarios like astrophysics, light travels across vast distances
nearly instantaneously due to c's enormous value.
In practical terms, the speed of light determines how quickly signals move across vast scales, such as in communication
and astronomy. It also plays a key role in spacetime's theory, particularly in special relativity.
The precise value is derived through detailed calculations from [Maxwell's equations, which
describe electric and magnetic fields. Without c being this high, time dilation and relativistic effects
would be negligible compared to the universe']s movement relative to light speed.
In summary, the speed of light remains a constant, significantly impacting various areas of physics and our
understanding of the universe."
Wow that's a lot! I think this is an example of what many people refer to as AI slop. Whatever else it says, however, the model seems to be fairly sure that the speed of light is 299,792,458 meters per second which is correct according to wikipedia.
This is a very small version of the DeepSeek model but it can still do useful things and is a fun and interesting way to learn about both the strengths and weaknesses of LLM-based AI technology.
Have a play and tell me what you think.
- Category:
- artificial intelligence (AI)







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.