Earlier this week I posted a summary of posts from the beginning of this blog, including my January 13, 2006 post on generating test images. Today I want to revisit one of the examples from that old post.

In my 2006 post I showed this test image, consisting of concentric rings with increasing frequency as you move away from the center of the image:

Since then I have seen this type of image referred to as the Jähne test pattern. This week I decided to go looking for the source of this reference, and I found a very similar image described in Practical Handbook on Image Processing for Scientific and Technical Applications, by Bernd Jähne, CRC Press, 1997. Here's a scan of Figure 10.23a, page 348, from that book:

The test image is constructed using equation (10.63):

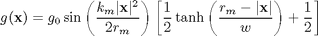
where is the vector offset from the image center, is therefore the distance from the image center, and 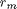is the maximum value of in the image.

Today I'm going to ignore the second term (tanh) and just focus on the first term, and I'm going to substitute for . The instantaneous frequency of the sinusoid is given by:

The maximum instantaneous frequency, which occurs when , is therefore 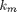. For a discrete signal defined on a grid with unit spacing, the maximum representable frequency is , which corresponds to a period of 2 units.

OK, let's try it.

km = pi;
[x,y] = meshgrid(-200:200);
r = hypot(x,y);
rm = max(r(:));

g = sin( (km * r.^2) / (2 * rm) );
imshow(g,[])

I used the autoscaling syntax of imshow because the values of g range from -1 to 1. We can scale and shift g to get it into the range [0,1]. Then we don't need the second input to imshow, and the image will write out correctly if we use imwrite.

g = (g + 1)/2;
imshow(g)

Just for fun, let's push the maximum instantaneous frequency way past reasonable and look at the resulting aliasing artifacts.

km = 4*pi;
g = sin( (km * r.^2) / (2 * rm) );
g = (g + 1) / 2;
imshow(g)

I spent really much too long playing with this image yesterday, so I'm going to subject you to one or two more posts about it. For one thing, having the instantaneous frequency vary directly with distance from the image means we can explore interesting effects using bandpass filters. For another, I want to come back to the tanh term in the equation from Jähne's book. I'm a bit puzzled by it.

Get the MATLAB code

Published with MATLAB® 7.12