Image-based graphs
Last time I showed you the basics of using the new graph theory functionality in MATLAB R2015b. Today I want to talk about some functions I put on the File Exchange for making graphs from images. Those of you working with graph-based image analysis algorithms might find them useful. I would be very interested in receiving feedback on these functions.
The function imageGraph creates a graph representing the neighbor relationships for every pixel in an image with a specified size. imageGraph3 does the same thing for a 3-D image array.
The function binaryImageGraph creates a graph representing the neighbor relationships for every foreground pixel in a binary image. binaryImageGraph3 creates a graph from a 3-D binary image array.
The function plotImageGraph plots a graph created by imageGraph or binaryImageGraph with the graph nodes arranged on a pixel grid.
Finally, the function adjacentRegionGraph creates a graph from a label matrix defining image regions. The graph represents the region adjacency relationships.
Contents
Example: Image graph with 8-connected pixels
Create a graph for a 480-by-640 image with 8-connected pixels.
g = imageGraph([480 640],8)
g =
graph with properties:
Edges: [1225442x2 table]
Nodes: [307200x3 table]
Graph nodes contain the x-coordinate, y-coordinate, and linear index of the corresponding image pixels.
g.Nodes(1:5,:)
ans =
x y PixelIndex
_ _ __________
1 1 1
1 2 2
1 3 3
1 4 4
1 5 5
Plot the image graph using plotImageGraph.
plotImageGraph(g) axis([100 110 220 230])
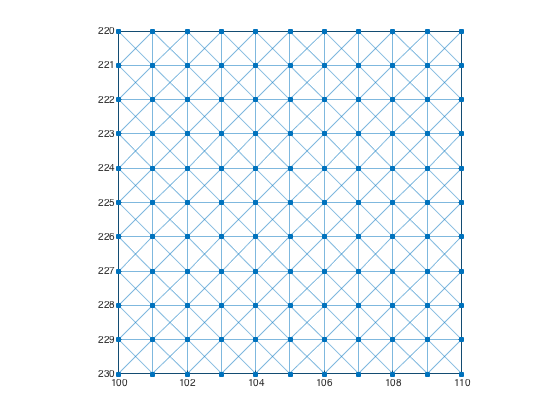
Example: Image graph with 4-connected pixels
Create a graph for a 480-by-640 image with 4-connected pixels.
g = imageGraph([480 640],4)
g =
graph with properties:
Edges: [613280x2 table]
Nodes: [307200x3 table]
plotImageGraph(g) axis([100 110 220 230])
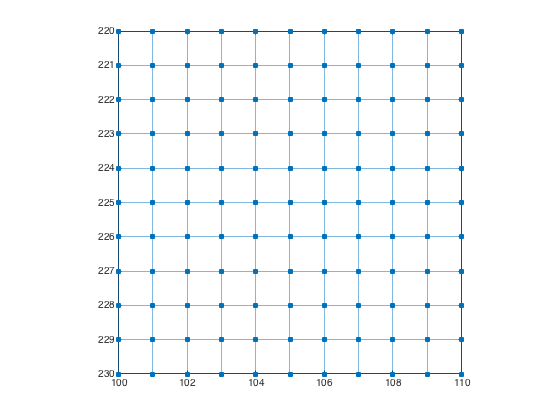
Example: Image graph with special connectivity
Use a 3-by-3 connectivity matrix to create an image graph with 6-connected pixels. Each pixel is connected to its north, northeast, east, south, southwest, and west neighbors.
conn = [0 1 1; 1 1 1; 1 1 0]; g = imageGraph([480 640],conn); plotImageGraph(g) axis([100 110 220 230])
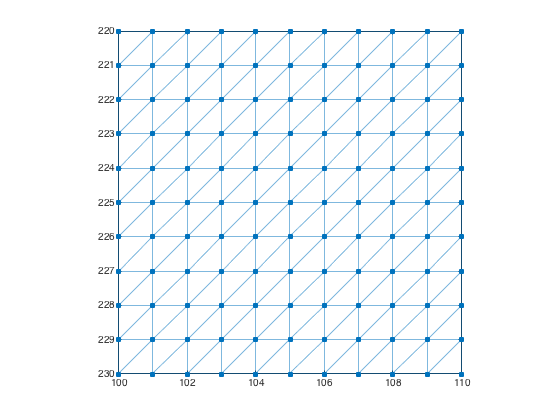
Example: Binary image graph
Create a graph whose nodes are the foreground pixels of the binary image text.png (a sample image that is included with the Image Processing Toolbox).
bw = imread('text.png'); imshow(bw) title('Original image')

g = binaryImageGraph(bw); figure plotImageGraph(g) axis([60 85 30 45])

Region Graphs
A label matrix defines a set of regions based on each unique element value in the matrix. For example, suppose you had the following label matrix:
L = [10 10 3 4.5 4.5; 10 10 3 4.5 4.5; 20 20 3 15 15; 20 20 3 15 15]
L = 10.0000 10.0000 3.0000 4.5000 4.5000 10.0000 10.0000 3.0000 4.5000 4.5000 20.0000 20.0000 3.0000 15.0000 15.0000 20.0000 20.0000 3.0000 15.0000 15.0000
This label matrix defines 5 regions:
- A 2-by-2 region in the upper left labeled with the value 10.
- A 2-by-2 region in the lower left labeled with the value 20.
- A one-pixel-wide vertical region in the middle labeled with the value 3.
- A 2-by-2 region in the upper right labeled with the value 4.5.
- A 2-by-2 region at the lower right labeled with the value 15.
The function adjacentRegionsGraph returns a graph with the same number of nodes as labeled regions. Edges in the graph indicate pairs of adjacent regions.
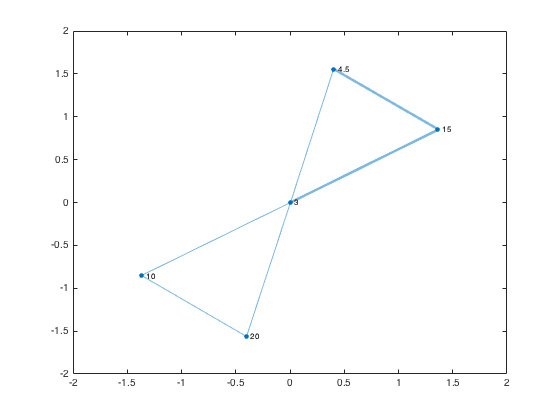
Example: Region graph
Compute an adjacent regions graph. Plot the graph, highlighting the nodes connected to the label 15.
g = adjacentRegionsGraph(L)
g =
graph with properties:
Edges: [6x2 table]
Nodes: [5x1 table]
The graph nodes contain the region labels.
g.Nodes
ans =
Label
_____
3
4.5
10
15
20
The graph edges contain the labels for each adjacent region pair.
g.Edges
ans =
EndNodes Labels
________ __________
1 2 3 4.5
1 3 3 10
1 4 3 15
1 5 3 20
2 4 4.5 15
3 5 10 20
Plot the graph, capturing the GraphPlot object as an output argument.
gp = plot(g,'NodeLabel',g.Nodes.Label)
gp =
GraphPlot with properties:
NodeColor: [0 0.4470 0.7410]
MarkerSize: 4
Marker: 'o'
EdgeColor: [0 0.4470 0.7410]
LineWidth: 0.5000
LineStyle: '-'
NodeLabel: {'3' '4.5' '10' '15' '20'}
EdgeLabel: {}
XData: [0.0011 0.4051 -1.3642 1.3629 -0.4048]
YData: [0.0015 1.5564 -0.8540 0.8538 -1.5577]
Use GET to show all properties
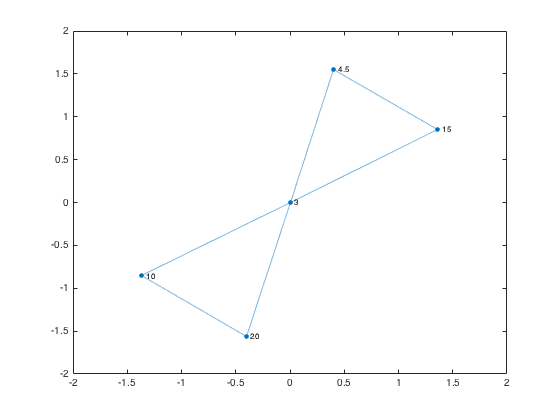
Find the neighbors of the region labeled 15.
node_num = find(g.Nodes.Label == 15); neighbors_15 = neighbors(g,node_num); highlight(gp,node_num,neighbors_15)
Next time I plan to show you a graph-based maze solver ... that cheats.
I'd love for you try Image Graphs. Please let me know what you think.
Copyright 2015 The MathWorks, Inc.
Published with MATLAB® R2015b









コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。