Image-based graphs
Last time I showed you the basics of using the new graph theory functionality in MATLAB R2015b. Today I want to talk about some functions I put on the File Exchange for making graphs from images. Those of you working with graph-based image analysis algorithms might find them useful. I would be very interested in receiving feedback on these functions.
The function imageGraph creates a graph representing the neighbor relationships for every pixel in an image with a specified size. imageGraph3 does the same thing for a 3-D image array.
The function binaryImageGraph creates a graph representing the neighbor relationships for every foreground pixel in a binary image. binaryImageGraph3 creates a graph from a 3-D binary image array.
The function plotImageGraph plots a graph created by imageGraph or binaryImageGraph with the graph nodes arranged on a pixel grid.
Finally, the function adjacentRegionGraph creates a graph from a label matrix defining image regions. The graph represents the region adjacency relationships.
Contents
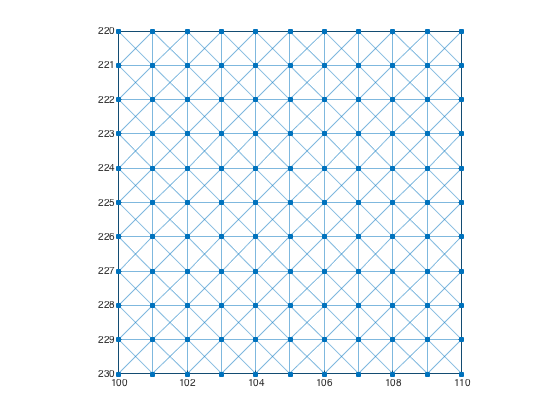
Example: Image graph with 8-connected pixels
Create a graph for a 480-by-640 image with 8-connected pixels.
g = imageGraph([480 640],8)
g =
graph with properties:
Edges: [1225442x2 table]
Nodes: [307200x3 table]
Graph nodes contain the x-coordinate, y-coordinate, and linear index of the corresponding image pixels.
g.Nodes(1:5,:)
ans =
x y PixelIndex
_ _ __________
1 1 1
1 2 2
1 3 3
1 4 4
1 5 5
Plot the image graph using plotImageGraph.
plotImageGraph(g) axis([100 110 220 230])
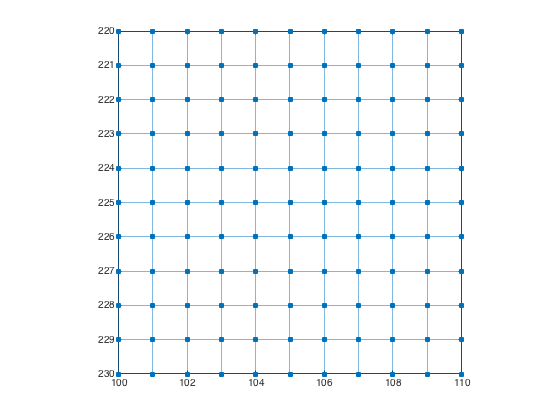
Example: Image graph with 4-connected pixels
Create a graph for a 480-by-640 image with 4-connected pixels.
g = imageGraph([480 640],4)
g =
graph with properties:
Edges: [613280x2 table]
Nodes: [307200x3 table]
plotImageGraph(g) axis([100 110 220 230])
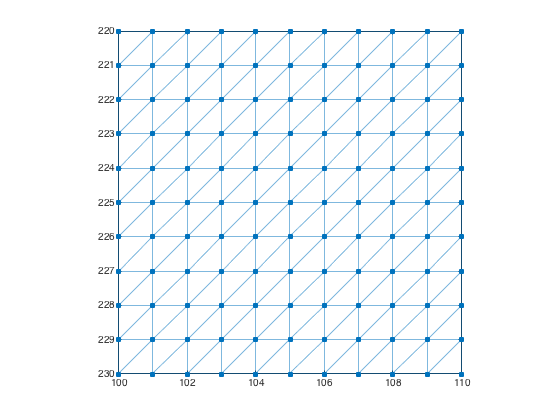
Example: Image graph with special connectivity
Use a 3-by-3 connectivity matrix to create an image graph with 6-connected pixels. Each pixel is connected to its north, northeast, east, south, southwest, and west neighbors.
conn = [0 1 1; 1 1 1; 1 1 0]; g = imageGraph([480 640],conn); plotImageGraph(g) axis([100 110 220 230])
Example: Binary image graph
Create a graph whose nodes are the foreground pixels of the binary image text.png (a sample image that is included with the Image Processing Toolbox).
bw = imread('text.png'); imshow(bw) title('Original image')

g = binaryImageGraph(bw); figure plotImageGraph(g) axis([60 85 30 45])

Region Graphs
A label matrix defines a set of regions based on each unique element value in the matrix. For example, suppose you had the following label matrix:
L = [10 10 3 4.5 4.5; 10 10 3 4.5 4.5; 20 20 3 15 15; 20 20 3 15 15]
L = 10.0000 10.0000 3.0000 4.5000 4.5000 10.0000 10.0000 3.0000 4.5000 4.5000 20.0000 20.0000 3.0000 15.0000 15.0000 20.0000 20.0000 3.0000 15.0000 15.0000
This label matrix defines 5 regions:
- A 2-by-2 region in the upper left labeled with the value 10.
- A 2-by-2 region in the lower left labeled with the value 20.
- A one-pixel-wide vertical region in the middle labeled with the value 3.
- A 2-by-2 region in the upper right labeled with the value 4.5.
- A 2-by-2 region at the lower right labeled with the value 15.
The function adjacentRegionsGraph returns a graph with the same number of nodes as labeled regions. Edges in the graph indicate pairs of adjacent regions.
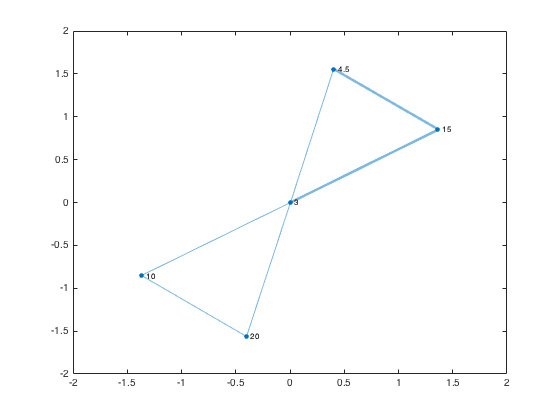
Example: Region graph
Compute an adjacent regions graph. Plot the graph, highlighting the nodes connected to the label 15.
g = adjacentRegionsGraph(L)
g =
graph with properties:
Edges: [6x2 table]
Nodes: [5x1 table]
The graph nodes contain the region labels.
g.Nodes
ans =
Label
_____
3
4.5
10
15
20
The graph edges contain the labels for each adjacent region pair.
g.Edges
ans =
EndNodes Labels
________ __________
1 2 3 4.5
1 3 3 10
1 4 3 15
1 5 3 20
2 4 4.5 15
3 5 10 20
Plot the graph, capturing the GraphPlot object as an output argument.
gp = plot(g,'NodeLabel',g.Nodes.Label)
gp =
GraphPlot with properties:
NodeColor: [0 0.4470 0.7410]
MarkerSize: 4
Marker: 'o'
EdgeColor: [0 0.4470 0.7410]
LineWidth: 0.5000
LineStyle: '-'
NodeLabel: {'3' '4.5' '10' '15' '20'}
EdgeLabel: {}
XData: [0.0011 0.4051 -1.3642 1.3629 -0.4048]
YData: [0.0015 1.5564 -0.8540 0.8538 -1.5577]
Use GET to show all properties
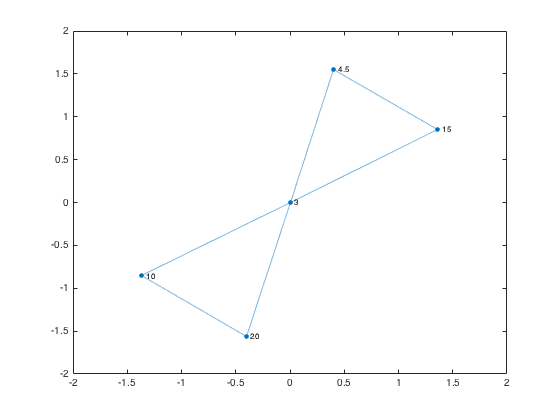
Find the neighbors of the region labeled 15.
node_num = find(g.Nodes.Label == 15); neighbors_15 = neighbors(g,node_num); highlight(gp,node_num,neighbors_15)
Next time I plan to show you a graph-based maze solver ... that cheats.
I'd love for you try Image Graphs. Please let me know what you think.
Copyright 2015 The MathWorks, Inc.
Published with MATLAB® R2015b
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.