Related Content on the File Exchange
Question: How do you find what you’re not necessarily looking for?
Answer: You look at the related content listed under the heading “Others Also Downloaded”
We recently added a new “related content” feature to the File Exchange. It helps you move smoothly from one item to other related items. I find that it supports a discovery workflow… that is, one where you start out with one idea about what you want to do, but it morphs organically into something different but better. Let me to illustrate with a story.
I like airplanes. Many years ago I trained as an aerospace engineer. That’s how I came to learn MATLAB! Anyway, here’s a picture of an airplane coming in for a landing.

It doesn’t look very well aligned with the runway, but what should we tell the pilot to do? How can we precisely define the orientation of the plane relative to the runway? In order to model our plane, we need a way to specify its orientation. For this, we use Euler angles. Euler angles are named after mathematical superhero Leonhard Euler, and since his last name sounds like “Oiler”, I always thought his hometown of Basel, Switzerland should have a hockey team named the Basel Eulers. But that’s not what I came here to talk about.
Euler angles can be used for any object, but they’re especially useful when the object you’re describing is unglued from any fixed reference frame. For a car moving in (more or less) two dimensions, you may not need to worry about much more than the compass heading (azimuth). Gravity keeps the vehicle on the ground. But things like airplanes and spacecraft can point in any direction. So we might use the angles yaw (for heading) followed by pitch (for the elevation of the nose) followed by roll (for the twist around the long axis). These are the Euler angles.
It’s hard to visualize how these angles work, so let’s apply some MATLAB. And rather than write something ourselves, let’s look on the File Exchange. After a quick search for Euler angles, this title caught my eye: SpongeBob Squarepants goes 3-D by Antonio Tristán Vega of the Universidad de Valladolid in Spain. Antonio knows that SpongeBob can brighten any task, including modeling the orientation of a rigid body in 3-space.
I downloaded it, installed it (it depends on two other submissions) and ran it. This is what I saw.
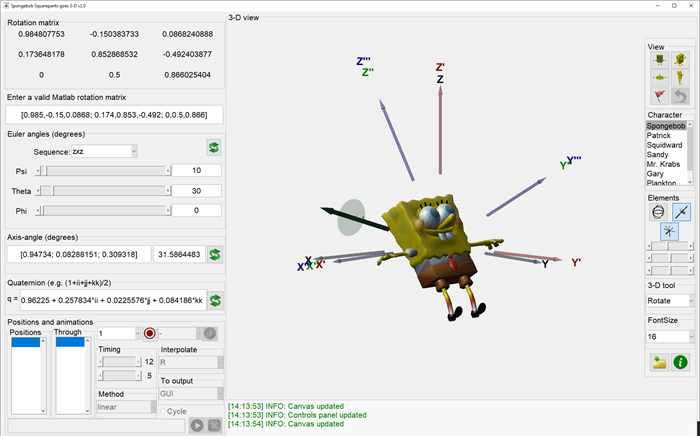
I played around with that for a little bit. It’s nice! But I also noticed, on the File Exchange page for this entry, there was a little box off to the right, just below the tags: “Others Also Downloaded”. It shows you other files downloaded by the people who downloaded this file. This shows me related content and saves me the hassle of going back to the search results page.
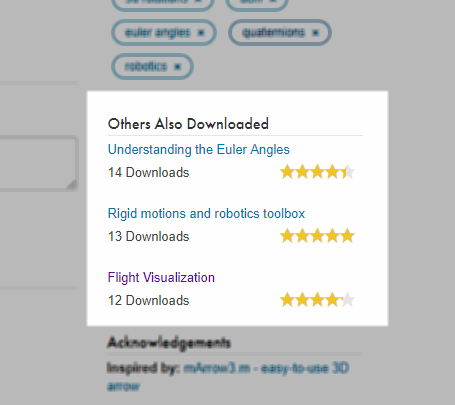
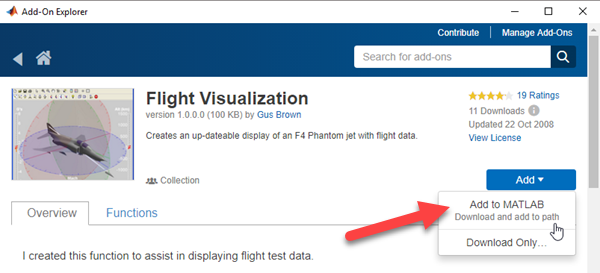
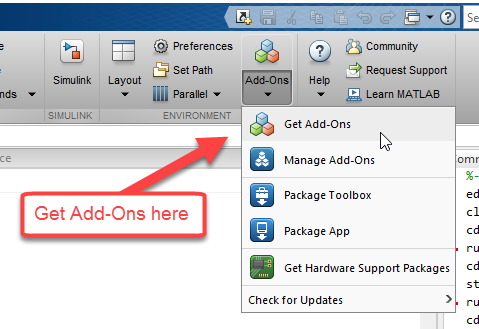
Third on the list above was the Flight Visualization entry by Gus Brown. It looked like fun. It wasn’t what I was originally looking for, but I wanted to give it a try. This time, I decided to download it directly from inside MATLAB using the Add-On Explorer. The Add-On Explorer is basically an in-product view of the File Exchange. It shows you all the same content, but when you click on the Add button, it has the advantage of downloading the entry, installing it, and putting it on the path in one click. Super convenient.
After I got it running, here’s what the Flight Visualization entry looks like on my computer.
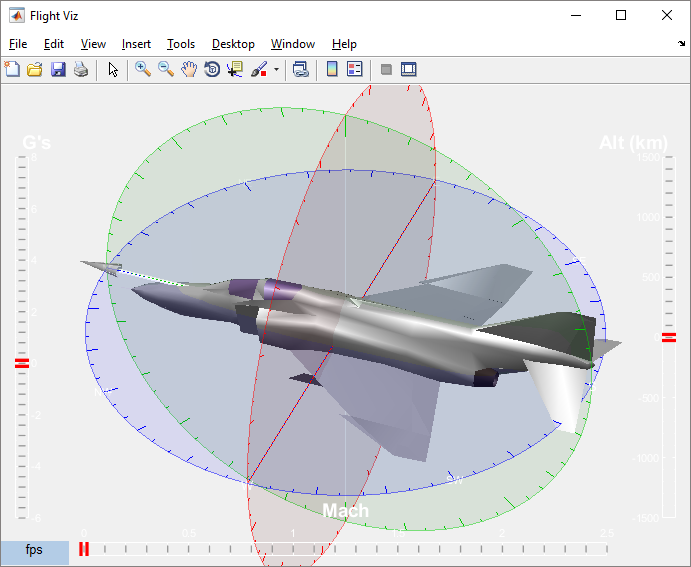
Pretty slick! That F-4 Phantom looks a little more aerodynamic than SpongeBob. I played with the F-4, but once again my wandering eye found the related content section of the page.
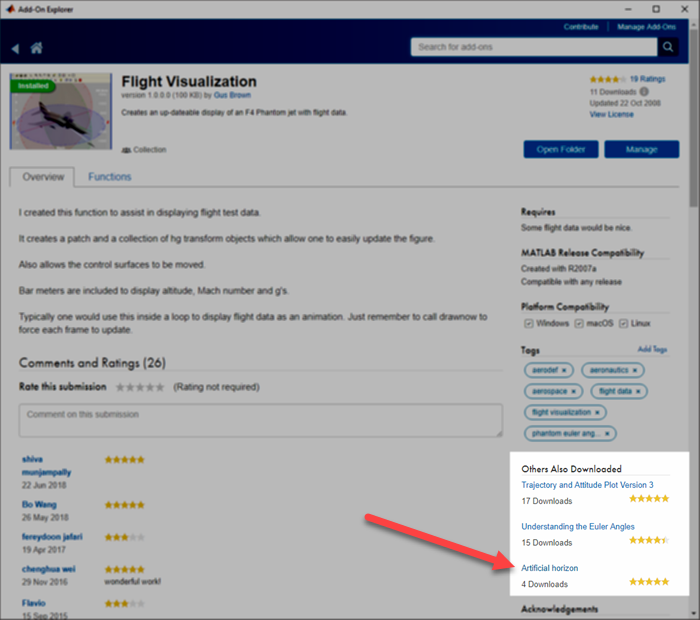
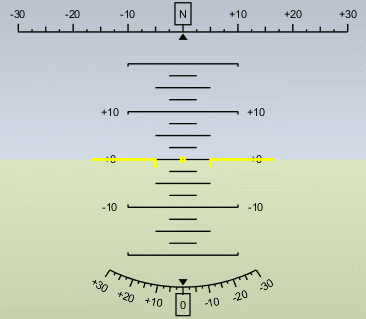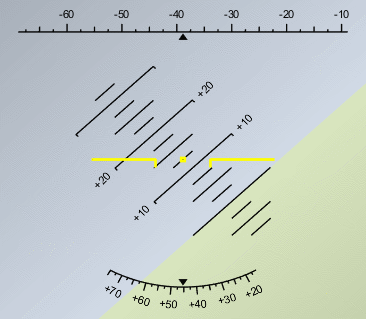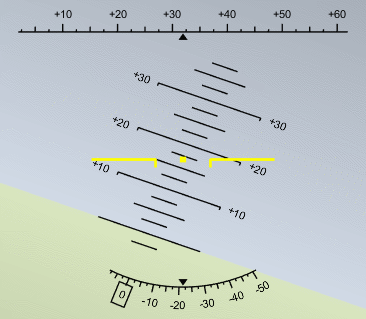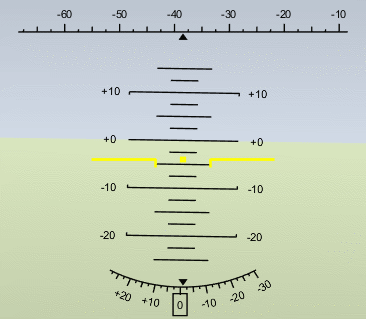
Artificial Horizon, eh? That’s worth a look. I clicked on link and installed the file, and I was soon looking at a MATLAB version of the cockpit instrument that shows a plane’s orientation. The file was authored by Eric Ogier.
Naturally, I wanted to put it through its paces. I wanted to show it with some real flight data. But where to get the data? That’s when I had a fantastic brainstorm: I could generate my own flight data with MATLAB Mobile! I fired up my copy of MATLAB Mobile and connected it to my desktop MATLAB via the Connector. Then I went to the Sensors page of the app and started up streaming of Azimuth, Pitch, and Roll (our old Euler angle friends) to MATLAB.
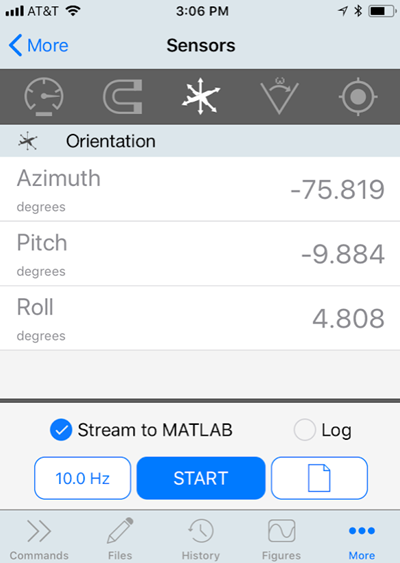
Then all I had to do was fly my phone around like a plane for a few seconds. Literally flying my phone around the office going VROOM VROOM. The data streamed into MATLAB, and I was quickly able to visualize the result with the Artificial Horizon code. Here is an animation of the result.
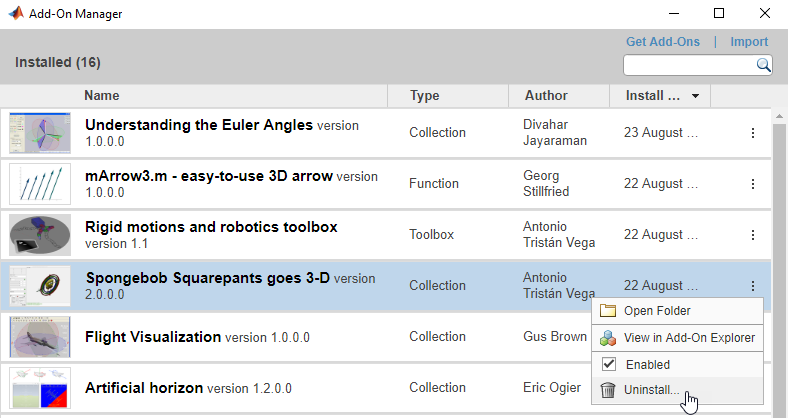
So there you have it. An improbable journey of discovery powered by the ability to see related content and quickly install it. And I should point out, now that I’m done with this task, the Add-On Manager also makes it easy to UNINSTALL the files you’re done with. Easy come, easy go. Just the way it should be.







コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。