Leap Days on Mars
February 29th is right around the corner. It’s been hibernating for the past three years, snuggling in its secret den between February 28th and March 1st. But it’s just about to emerge again, stretching the calendar and irritating impatient March.

The name March comes from the Latin Martius mensis, or “month of Mars.” This connection between leap year and Mars got me thinking: do they have leap years on Mars? After all, it won’t be too long before humans are living on Mars. They’re going to have to worry about these things. Otherwise they might forget that February has 51 days this year and they’ll end up at the post office on a bank holiday.
The first thing you have to do is think about what a leap year is doing for you. It feels kind of medieval, doesn’t it? Like, it’s 2020 and we’re still hammering 24 extra hours into February because… why? Let’s break it down. A leap year is a year in which an extra day is inserted. Something bad will happen if you don’t. But what?
The key realization is that we have two “natural” ways of measuring time. Two different clocks. One clock is the rate at which the earth goes around the sun: the year. The other clock is the rate at which the earth spins on its axis: the day. These clocks don’t know about each other, so there’s no reason for them to be synchronized. Nothing physical compels an integer number of days to fit into a year. But for the purposes of our human calendar, we need to make them fit together. So we have to do some error-correction.
So now let’s have a little fun with MATLAB.
Leap Days on Earth
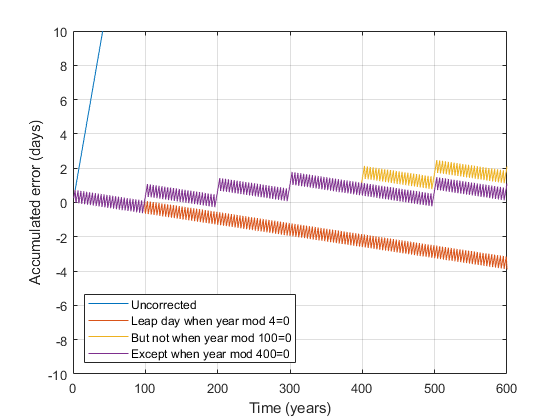
We can say that one year is 365 days, but really, one year is 365.2425 days (more or less). So a 365 day calendar will pile up around one day worth of error every four years. Wait long enough and the error can become substantial. After 360 years, your seasons will lag the calendar by three months. The Romans figured this out and added the extra day every four years.
But even this correction isn’t perfect. We need to remove 3 leap days every 400 years to make things fit reasonably well. So if a year is evenly divisible by 100, it’s not a leap year, unless it’s also divisible by 400.
maxYrs = 600; yrs = 1:maxYrs; % This is the actual error that will crop up err = 0.2425*yrs; mods = [~mod(yrs,4); -~mod(yrs,100); ~mod(yrs,400)]; allMods = sum(mods); % This is our approximation of the error cumErr = sum(allMods)/maxYrs
cumErr = 0.2417
plot(err) hold on plot(err - cumsum(mods(1,:))) plot(err - cumsum(sum(mods(1:2,:)) )) plot(err - cumsum(sum(mods(1:3,:)) )) hold off xlabel('Time (years)') ylabel('Accumulated error (days)') ylim([-10 10]) grid on legend({ ... 'Uncorrected', ... 'Leap day when year mod 4=0', ... 'But not when year mod 100=0', ... 'Except when year mod 400=0'}, ... 'Location','southwest')
Martian Leap Days
Now what about Mars? Does it have the same problem? Yes it does. A Martian year is made up of 668.599 Martian days, or sols. So we need some calendar correction if we’re going to fit sols evenly into years. One way to do it is to make years 668 sols long unless the year is evenly divisible by 2 or 5. On average you can see this works out to 668.6. To this rule we can add a refinement. If the year is also divisible by 1000, don’t apply the leap day.
maxYrs = 1500; yrs = 1:maxYrs; err = 0.599*yrs; mods = [~mod(yrs,2); ~mod(yrs,5); ~mod(yrs,1000)]; allMods = any(mods(1:2,:) - mods(3,:)); cumErr = sum(allMods)/maxYrs
cumErr = 0.5993
plot(err) hold on plot(err - cumsum(mods(1,:))) plot(err - cumsum(any(mods(1:2,:)))) plot(err - cumsum(any(mods(1:2,:))) + cumsum(mods(3,:))) hold off xlabel('Time (years)') ylabel('Accumulated error (days)') ylim(10*[-1 1]) grid on legend({ ... 'Uncorrected', ... 'Leap day when year mod 2=0', ... 'Also when year mod 5=0', ... 'Except when year mod 1000=0'}, ... 'Location','southwest')

Leap Day Fun with Primes
By now you see this whole leap day process is simply an exercise in using rational numbers to approximate the weird decimal constants dictated to us by the universe. There’s no magic to it, and it can be managed in a number of different ways. So even though the Martian leap year scheme shown above seems solid, I’d like to propose a more elegant solution. And by “elegant” I mean that it is actually more complicated, but involves more prime numbers.
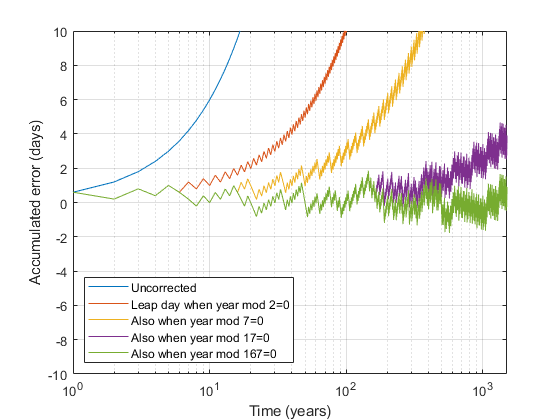
Here goes (ahem): A Martian year is 668 sols long unless it is evenly divisible by 2, 7, 17, or 167, in which case a leap day is added between February 50th and March 1st. Since March is the month named after the planet, I think we should in fact call this leap day March 0th.
maxYrs = 1500; yrs = 1:maxYrs; err = 0.599*yrs; mods = [~mod(yrs,2); ~mod(yrs,7); ~mod(yrs,17); ~mod(yrs,167)]; allMods = any(mods); cumErr = sum(allMods)/maxYrs
cumErr = 0.5987
plot(err) hold on plot(err - cumsum(mods(1,:))) plot(err - cumsum(any(mods(1:2,:)))) plot(err - cumsum(any(mods(1:3,:)))) plot(err - cumsum(any(mods(1:4,:)))) hold off xlabel('Time (years)') ylabel('Accumulated error (days)') ylim(10*[-1 1]) grid on legend({ ... 'Uncorrected', ... 'Leap day when year mod 2=0', ... 'Also when year mod 7=0', ... 'Also when year mod 17=0', ... 'Also when year mod 167=0'}, ... 'Location','southwest')

Is that beautiful or what?
Just for fun, let’s look at those growing errors on a log scale.
set(gca,'XScale','log')
I’ll close by saying that right now there are no leap years on Mars, because there are no people. Leap years are human cultural constructs that come about because we need to make an integer number of days fit into a calendar year. As soon as humans start living on Mars, they will bring leap years with them, along with orange juice, yoga mats, and selfie sticks. And as funny as it sounds now, all the issues discussed here will matter to them. I wish them luck. Happy Leap Year!









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.