Cookies & Code
Seasonal greetings of the Greater Solstice Metropolitan Area! As I write this, the solstitial sun sets on the shortest day of my northern hemispheric year. Winter is here. So naturally, my mind turns to cookies.

The inspiration for this winter daydream comes from some code written by Eric Ludlam. Eric, in addition to being in charge of the MATLAB graphics team, is an inveterate tinkerer. He loves making fun graphics code. You may remember some of his pumpkin-inspired creations that I described in this space last year. Or you may recall his many entries from the latest Mini Hack (and the one before that).
He's back, this time with code for seasonal cookies and snowflakes. If you want to look at his code, you can find it in his Digital Art with MATLAB repo. In fact, let's go look at it now.
We can start by cloning our own copy in MATLAB. You can do this directly from the Current Folder Browser. Select "Manage Files..." from the Source Control context menu.
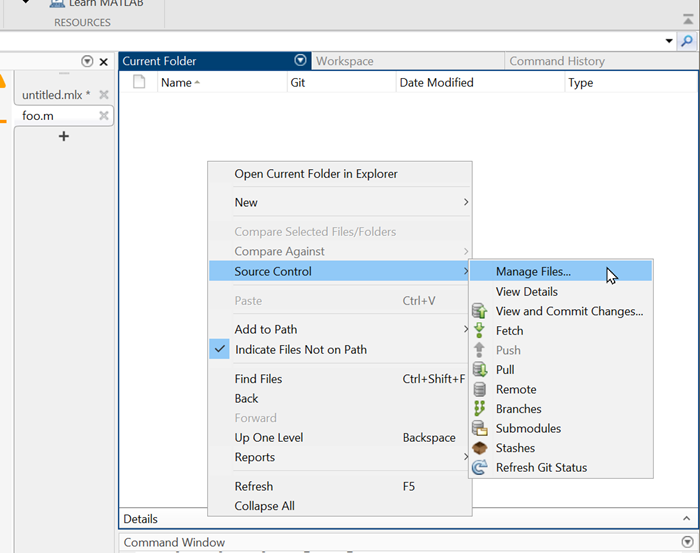
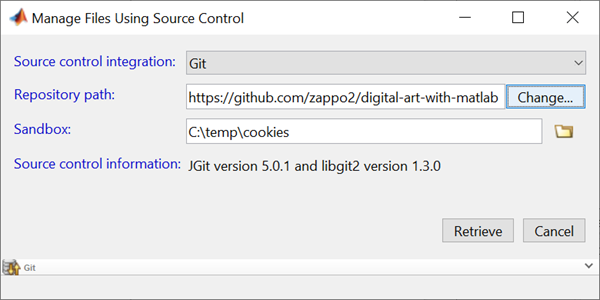
Enter the Repository Path (https://github.com/zappo2/digital-art-with-matlab), and the files come right down.
Eric made some cookie code using blobby implicit surfaces as described by Jim Blinn. We can use Eric's template as cookie-cutter (heh) to stamp out other designs. Shown below is the code from gingerbreadperson.m, only I've substituted my own design at the top: a candy cane.
% Create a gingerbread person cookie
K = [' xxx '
' xxxxx '
' xxx xxx '
' xxx xxx '
'xxx xxx '
'xxx xxx '
'xxx xxx '
' xxx '
' xxx '
' xxx '
' xxx '
' xxx '
' xxx '];
% Convert K into array of blob centers
[y,x]=find(~isspace(K));
% Scale and offset centers into 3D cookie space
C=[x*5,y*5]+5; C(:,3)=10;
% Compute a volume using a short implementation of Blinn's blobs
nx=size(K,2)*5+10; ny=size(K,1)*5+10; nz=20; % Size of volume
[y,x,z]=ndgrid(1:ny,1:nx,1:nz);
vol=zeros(ny,nx,nz);
for i=1:size(C,1)
vol=vol+exp(-.05*((C(i,1)-x).^2 + (C(i,2)-y).^2 + (C(i,3)-z).^2));
end
% Compute isosurface from the blobs
S=isosurface(vol,.3);
% Draw the isosurface using patch
newplot
patch(S,'FaceColor','#a56c3c','EdgeColor','none'); % cookie
axis equal ij off
lighting gouraud
camlight
material([.6 .9 .3 ])
It's not the most shapely candy cane, but it will do. Let's add some icing.
newplot
patch(S,'FaceColor','interp','EdgeColor','none','FaceVertexCData',S.vertices(:,3));
colormap(validatecolor({ '#a56c3c' '#f09090' }, 'multiple'));
clim([10 20]);
axis equal ij off
lighting gouraud
camlight
material([.6 .9 .3 ])
Obviously, it's easy to draw with X's into the variable K to make any cookie shape that pleases you. What happens if we make it random?
% Create a gingerbread blob
K = double(rand(10,10)>0.5);
K(K==0) = char('*');
K = char(K);
% Convert K into array of blob centers
[y,x]=find(~isspace(K));
% Scale and offset centers into 3D cookie space
C=[x*5,y*5]+5; C(:,3)=10;
% Compute a volume using a short implementation of Blinn's blobs
nx=size(K,2)*5+10; ny=size(K,1)*5+10; nz=20; % Size of volume
[y,x,z]=ndgrid(1:ny,1:nx,1:nz);
vol=zeros(ny,nx,nz);
for i=1:size(C,1)
vol=vol+exp(-.05*((C(i,1)-x).^2 + (C(i,2)-y).^2 + (C(i,3)-z).^2));
end
% Compute isosurface from the blobs
newplot
S=isosurface(vol,.3);
patch(S,'FaceColor','interp','EdgeColor','none','FaceVertexCData',S.vertices(:,3));
colormap(validatecolor({ '#a56c3c' '#8090f0' }, 'multiple'));
clim([10 20]);
axis equal ij off
lighting gouraud
camlight
material([.6 .9 .3 ])
I like my random cookies, and I'm now inclined to try some in the kitchen.
I'll close with Eric's snowflake code. Here's the default.
snowflake
axis off
But, just as with the cookies (and as with real-life snowflakes), we can opt for a random flake.
steps = randi(10,1,randi(8)+2)
snowflake(steps)
axis off
Happy holidays, and thanks for the cookies, Eric!














Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.