Laddergrams
MATLAB is good at math, of course, but it can also let you have some fun with words. Go to the Gaming > Word Games category of the File Exchange and you can find a variety of different word games.
I like laddergrams, and since I couldn't find any on the File Exchange, I thought I'd have some fun and write about them here. Laddergrams (also called Word Ladders) are a word game invented by Lewis Carroll in which you change one word into another by means of intermediate words that differ by exactly one character. He introduced the puzzle with this word pair: HEAD to TAIL.
So the challenge is this: how can you transform HEAD to TAIL one letter at a time? Here is his answer from 1879.

Can we write some MATLAB code that will find a solution to this problem?
This problem gives us a chance to play with the graph object in MATLAB. As is frequently the case, once you set up the problem correctly, it's a breeze to calculate laddergrams for any pair of words. We'll start by reading a list of English words into a string.
url = "https://raw.githubusercontent.com/first20hours/google-10000-english/master/google-10000-english.txt";
wordList = string(webread(url));
words = wordList.splitlines;
Extract all the words that are exactly 4 letters long.
keep = words.matches(lettersPattern(4));
words = words(keep);
numWords = length(words)
Let's alphabetize the list.
words = sort(words);
We want to build a graph that contains all these four-letter words. Each node is a word, and each edge connects two words that can be "bridged" in one laddergram step. Let's build the adjacency matrix.
Two words are connected by an edge if they differ by one and only one letter location. So HEAD and HEAL are connected. HEAD and HEED are connected. But HEAD and HERE are not, since you need to change two letters to get from one to the next.
adj = zeros(numWords);
for i = 1:numWords
for j = i:numWords
% Three letters must be exact matches
if sum(char(words(i))==char(words(j)))==3
% The matrix is symmetric (the graph is undirected), so we
% touch two locations in the adjacency matrix.
adj(i,j) = 1;
adj(j,i) = 1;
end
end
end
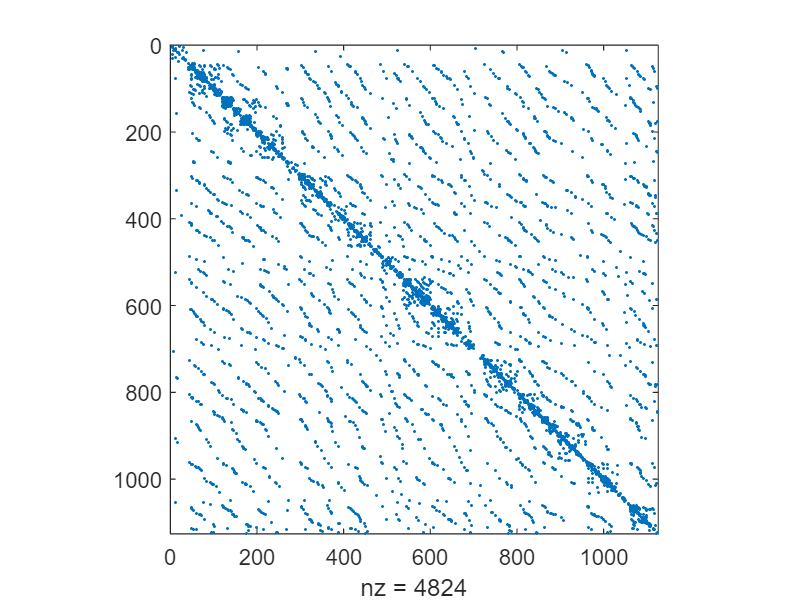
spy(adj)
The adjacency matrix has some fascinating structure! By marking the break between first letters, we can see what's going on a little better. We'll use the diff command to see where the first letter of each word changes.
ix = find(diff(char(words.extract(1)))~=0);
for i = 1:length(ix)
xline(ix(i))
yline(ix(i))
end
title("Word Connectivity Adjacency Plot")
Around index 800, you can see a very narrow strip that corresponds to Q. Only three 4-letter words in this dictionary start with Q: QUAD, QUIT, and QUIZ
Let's throw the alphabet on the plot's Y axis to make this more clear.
alphabet = ('a':'z')';
set(gca,YTick=ix, ...
YTickLabel=cellstr(alphabet))
Make the graph object.
g = graph(adj,words);
Calculate the distances between all the words. This is where the magic happens. This one command is incredible: effectively distances is solving every single potential word ladder. That's the beauty of tapping into the excellent libraries that are just waiting to be used in MATLAB. Any code I would come up with to solve this problem would take a long time to write and longer to run. Instead, BOOM! It's all done.
d = distances(g);
Some word pairs are relatively inaccessible, so they show up as infinitely far apart.
[word1ix,word2ix] = find(d==Inf);
Here are two words you will never be able to connect via laddergram, at least with this dictionary.
i = 10;
words([word1ix(i) word2ix(i)])
Or, as they say in Maine: You can't get there from here.
Let's zero out all those infinite edges so they don't confuse the rest of our calculations.
d(d==Inf) = 0;
And now a histogram to look at the numbers.
maxLadderLen = max(d(:))
histogram(d(:),1:maxLadderLen)
xlabel("Length of the Laddergram")
ylabel("Number of Word Pairs")
Six is the most common number of intermediate steps.
What are the longest possible word ladders?
[word1ix,word2ix] = find(d==max(d(:)));
length(word1ix)
i = 9;
p = shortestpath(g,word1ix(i),word2ix(i));
for j = 1:length(p)
fprintf("%s\n",words(p(j)))
end
There is a multi-way tie for longest laddergram (20 steps), but this champion word pair goes from TOWN to DRUM. As always, everything depends on the dictionary. A different dictionary can give vastly different results.
Finally, we can solve the problem that Lewis Carroll posed back in 1879.
p = shortestpath(g,"head","tail")'
Our words are different, but even with MATLAB on our side, we can't do better than Carroll did almost 150 years ago. But in the bargain, we've solved every single laddergram that can be represented in this dictionary.
numLaddergrams = nnz(d)/2
All 405,591 of them! I just love graph algorithms.











评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。