You may have seen the news on the MATLAB Blog that MATLAB Copilot has been updated to the GPT-5 mini model. My experience has shown this to be a huge improvement. So if you haven't tried Copilot yet, now's the time! It's only getting better. And it's nice to know that you don't have to wait for the next general release of MATLAB to get this improved version of Copilot. It's a service that gets better for everyone across the board. MATLAB is improving while you sleep!

I wanted to flex the latest Copilot, and an old problem came to mind that I remember from the Ancient Days: scattered data interpolation. Let's say I'm trying to make a 3D map of a mountain range. You've given me a list of measurements: altitudes for specific latitudes and longitudes, but in no particular order. What does the mountain range look like? This used to mean writing some non-trivial code, but about a dozen years ago we added the scatteredInterpolant function to MATLAB and life got easier. This built-in function makes the scattered data interpolation problem go away. But now it's even easier than that! I don't have to read the doc or even know that the function exists. I just go to Copilot and enter something like this.

Across a 2D domain, I have a set of randomly scattered measurements of 
altitude points. That is, for a list of (x,y) tuples, I know z. 
Help me turn this into a regularly sampled surface.

For my list of measurements, I'll be using random samples from a 3D surface. See if you can guess what it is!

% Determine the target shape. Choose mode number from k = 1..8.
k = 1;
m = 40;
L = membrane(k,m);

% Get random measurements across the surface
npts = 100;
ix = unique(randi(numel(L),[npts,1]));
[y,x] = ind2sub([n,n],ix);
z = L(ix);

Here are my measurements. With only 100 points, can you see the shape?

plot3(x,y,z,'.') 
axis vis3d

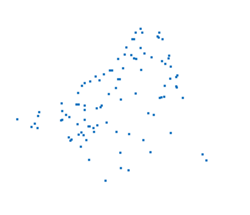
Let's animate it to make it pop a little better.

So let's make an interpolated shape. This next part is the code that Copilot gave me.

% Given column vectors x, y, z (all same length)
% Choose grid resolution
n = size(L,1);

% Grid covering the data range
xqv = linspace(min(x), max(x), n);
yqv = linspace(min(y), max(y), n);
[Xq, Yq] = meshgrid(xqv, yqv);

% Interpolate using scatteredInterpolant
F = scatteredInterpolant(x, y, z, 'natural');
Zq = F(Xq, Yq);

% Plot as surface (or use contourf/imagesc)
surf(Xq, Yq, Zq)
axis vis3d

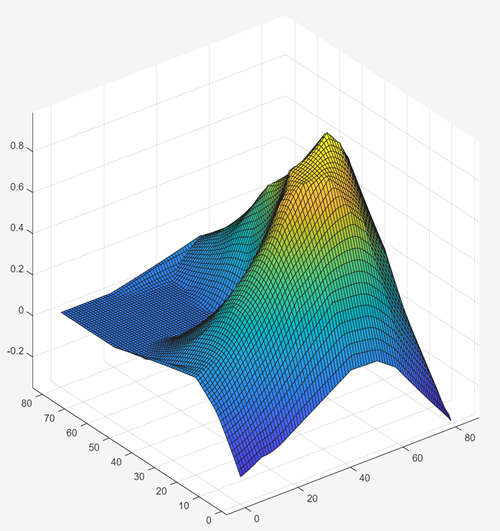
And there you have it! A slightly lumpy but recognizable reconstruction of the MathWorks logo (the output of membrane(1)) based on 100 randomly sampled points. Copilot made short work of my problem, giving me exactly what I was after. But all this playing around with scattered interpolants has made me hungrier for more. I'm curious how many points I need in order to see a particular shape.

An Interpolation Game

Let's make a game inside a MATLAB app. For this, I'm going to switch gears. Since this is a more complex task, I want to use one of our new prompts and the MATLAB MCP server that can be installed with Claude Desktop (Learn more about how to set this up from Mike's blog). Having access to this server makes everything go much faster. Here's a sketch of the app interface I want Claude to create for me.

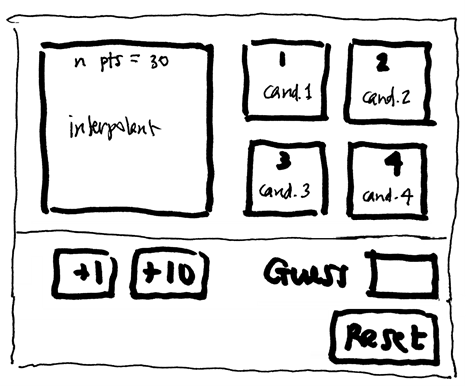
The idea is that there are four possible candidates that I'm sampling from. How many samples do I need to guess which of the four candidates is being sampled?

Writing an app can be a complicated exercise. But it doesn't have to be when AI is helping you. I'm going to use one of our new prompts that is especially designed to make app creation a breeze. I'll modify the prompt with these directions.

## Prompt for Interpolant Guessing Game
Create a MATLAB programmatic app for demonstrating 
scattered interpolants.

We will demonstrate interpolants with a guessing game: 
how many points do you need to guess the correct shape?

We are using a small number of points to interpolate 
across and unknown shape. We have four candidate surfaces 
to guess from. These will be four randomly chosen modes 
from among the first 8 modes of the L-shaped membrane 
(where mode n is returned by membrane(n)).

### The Layout
See the diagram in the file @sketch.png. On the left is a 
plot that shows the current interpolant. On the right are 
the four candidate shapes in a 2-by-2 grid.

The interpolant on the left will start out with 10 sample points. 
Underneath the interpolant plot are two buttons: "+1 sample" and 
"+10 samples". 

In the bottom right is a "Guess" editable text field where the 
user is invited to make a guess about which candidate shape is 
being interpolated. If they enter a value and press return, they
will be told if they are correct or incorrect.

Starting with the prompt from GitHub, I pasted the text shown here into the section called, appropriately, "The Prompt" to get a sort of super-prompt. Then I sent Claude on its way. Very quickly it gave me this.

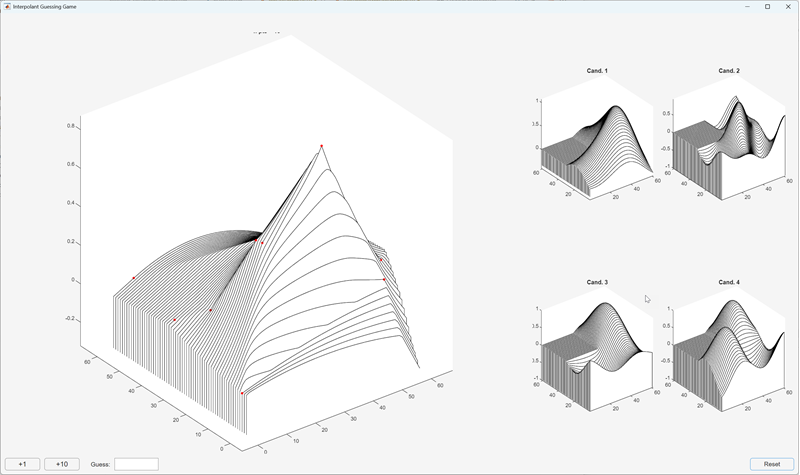
Nice! This is just what I was picturing. Everything worked as expected. I didn't have to worry about UI layout or button logic. It just worked. Here you're seeing an interpolation based on only 10 points. Which of the four potential candidates does this interpolated shape most likely match?

Now I'm going to use the buttons to add a bunch more measurements.

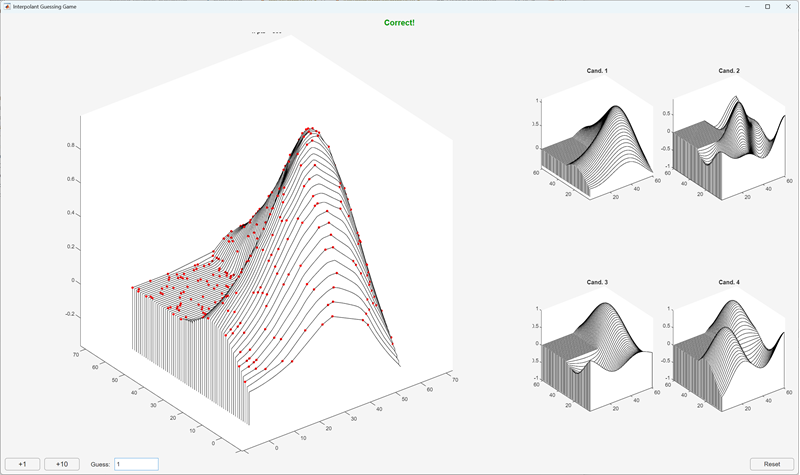
With 215 points, the fog has cleared. Can you see which candidate is being sampled? Why yes, it's Cleve Moler's old friend, the first vibrational mode of a membrane on a square domain with an invariant re-entrant corner, affectionately known around Natick as the L-shaped membrane. Looking good, Ellie!

It was fun exercising some basic MATLAB functionality using the latest Copilot. But then, leveraging the MCP Server, it was awesome to quickly create a game that builds on that learning and provides more insight about the nature of interpolation. AI lets you fly around a bigger design space. In the past, I would have had this same idea for a game, but I probably wouldn't have taken the time actually build it. Now it's more like the wave of a magical wand and VOOM! there it is.