Steve on Image Processing

At the European Colour in Graphics, Imaging, and Vision conference today, I took a tutorial called "Transforms for Colour and Spectral Reproduction." Mitch Rosen of the Munsell Color Science Laboratory, Rochester Institute of Technology, taught the class.

Mitch's topics included how to solve inverse problems in order to construct multidimensional lookup tables that transform colors from one space to another. One comment caught my ear - small approximation errors in these lookup tables can be relatively worse for colors that are neutral (gray) or near-neutral.

Let's explore this idea using the L*a*b* color space. L* is lightness, while a* and b* represent red-green and yellow-blue color differences, respectively. Colors for which a* and b* equal zero are neutral, or gray.

First let's look at a pair of reds that have the same luminance, and are separated by a distance of 20 in the a*-b* plane.

L = 85;
a = 70;
b = 0;

lab1 = [L a b];
lab2 = [L a+20 b];

Now convert these colors to sRGB space and display each as a single-pixel image.

cform = makecform('lab2srgb');
rgb1 = applycform(lab1, cform);
rgb2 = applycform(lab2, cform);

subplot(1,2,1)
imshow(reshape(rgb1,1,1,3))
title('L*a*b* = [85 70 0]')

subplot(1,2,2)
imshow(reshape(rgb2,1,1,3))
title('L*a*b* = [85 90 0]')

set(gcf, 'Color', 'w')

These colors are visibly different, but they have the same basic hue.

Now let's try the same thing with colors that are the same distance apart, but which are located close to the neutral axis.

lab3 = [85 10 0];
lab4 = [85 -10 0];

rgb3 = applycform(lab3, cform);
rgb4 = applycform(lab4, cform);

subplot(1,2,1)
imshow(reshape(rgb3,1,1,3))
title('L*a*b* = [85 10 0]')

subplot(1,2,2)
imshow(reshape(rgb4,1,1,3))
title('L*a*b* = [85 -10 0]')

set(gcf, 'Color', 'w')

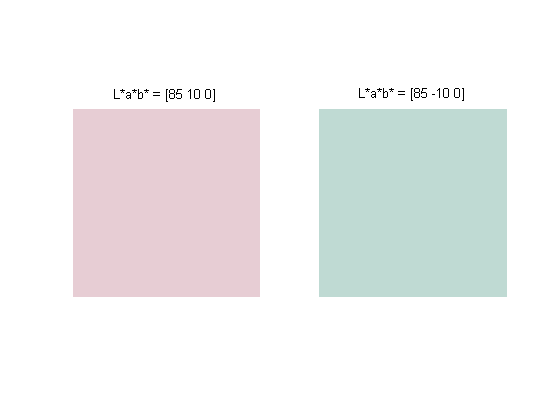
These colors have a distinctively different hue - one is pink and the other is green. The moral of the story is that "small" changes in a*-b* are more likely to produce dramatic hue shifts for colors close to the L*=0 axis.

Conference quote of the day: "In color science, if you want a real controversy, start a terminology discussion." - Jack Holm, Hewlett-Packard

Get the MATLAB code

Published with MATLAB® 7.2