OK, I've learned an important lesson about this blog: I really shouldn't start up two topics series at the same time. It's too hard to find the time to compose posts on both topics each week, and so the frequency of my posts drops off.

Anyway, let's get into the third algorithm for labeling connected components in a binary image. It involves two passes over the image, with an in-between step called equivalence class resolution. I first learned about this idea from Haralick and Shapiro, Computer and Robot Vision, vol. I, Addison-Wesley, 1992.

The first pass assigns temporary labels to each foreground pixel. Here's a graphical illustration of that procedure, using this small sample image:

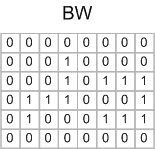
Now scan the image, processing one pixel at a time. Because of the way MATLAB stores matrix elements in memory, we'll scan along columns. When the scan encounters a foreground pixel, look at that pixel's neighbors that have already been encountered in the scan. Here's the first foregound pixel encountered, shown with its already-scanned neighbors highlighted in color:

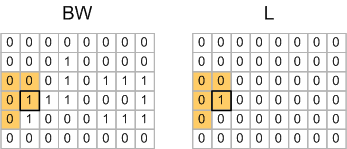
For the pixel shown above, none of the highlighted neighbors have been assigned a temporary label yet, so a new label value (1) is assigned to the corresponding pixel in the output.

Here's the second foregound pixel encountered:

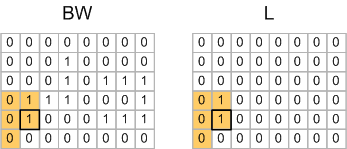
Note that one of this pixel's neighbors has already received a label (1), so this pixel is also assigned a temporary label of 1 in the output image.

When the scan gets to row 2, column 4 pixel, none of that pixel's scanned neighbors have been labeled, so that pixel gets assigned a new temporary label of 2.

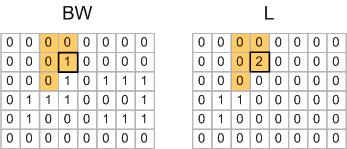
The very next pixel, on row 3, column 4, is where things start to get more interesting:

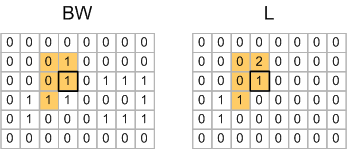
One of this pixel's scanned neighbors has already been assigned a label of 1, but another of the neighbors has been assigned a label of 2. So the algorithm picks one of the labels arbitrarily, and then records the fact that temporary label 1 and temporary label 2 actually refer to the same object.

This situation happens again on row 4, column 8:

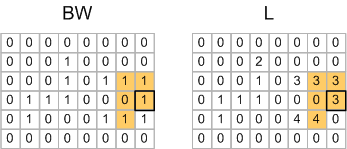
So the pair of labels 3 and 4 is an equivalence and goes into the equivalence table.

When the first pass is done, you have this matrix of labels:

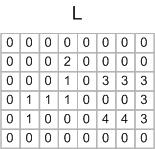
And you have an equivalence table containing these pairs:

 1 <--> 2
 3 <--> 4

Equivalence class resolution is the process of determining which subsets of the temporary labels really refer to the same object. You can do that in MATLAB using the technique I showed previously that was based adjacency matrix and dmperm. From this you would compute that temporary labels 1 and 2 map to final label 1, and temporary labels 3 and 4 map to final label 2. Then you make a second pass over the output matrix to relabel the pixels according to this mapping:

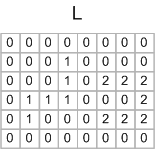
The Image Processing Toolbox function bwlabeln uses a variation of this technique, where the equivalence class resolution is actually performed during the first pass, using an algorithm called union find. I'll explain that next time.

Get the MATLAB code

Published with MATLAB® 7.4