a* and b*
Note added 27-Apr-2021: See the updated discussion of this topic in the 27-Apr-2021 post, "Plotting a* and b* colors."
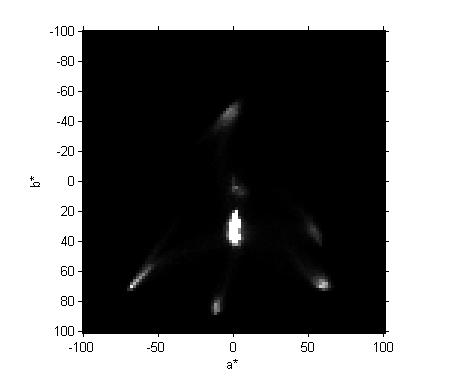
Last week I showed how to compute a two-dimensional histogram. Specifically, I computed the two-dimensional histogram of the a*-b* values of this image:

This was the result:
Blog reader Vanessa naturally wanted to know what this all means. (And blog reader Cmac gave a pretty good answer.)
Let me elaborate a bit. By L*a*b* I refer to the CIE 1976 L*, a*, b* color space. Here's a description of the three dimensions (from the Wikipedia article):
"The three coordinates of CIELAB represent the lightness of the color (L* = 0 yields black and L* = 100 indicates diffuse white; specular white may be higher), its position between red/magenta and green (a*, negative values indicate green while positive values indicate magenta) and its position between yellow and blue (b*, negative values indicate blue and positive values indicate yellow). The asterisk after L, a and b are part of the full name, since they represent L*, a* and b*, to distinguish them from Hunter's L, a and b, [an earlier color space]."
Bright spots in the two-dimensional histogram indicate that a relatively large number of pixels in the original image have the corresponding a* and b* values.
Consider, for example, the lowest bright spot on the two-dimensional histogram. By using impixelinfo and my mouse I was able to see that the a* and b* values for this spot are about -12 and 85. What color is that? To convert back to RGB values that we can display I have to pick some value for L*, whose natural range is 0 to 100. I'll pick 90, a fairly bright value. Then I use applycform to convert from L*a*b* to sRGB.
lab = [90 -12 85];
rgb = applycform(lab, makecform('lab2srgb'))
rgb =
0.9297 0.9066 0.0971
How can we look at this color? There are a lot of different ways. One procedure is to display a 1-by-1 indexed image with a one-color colormap.
image(1) colormap(rgb)
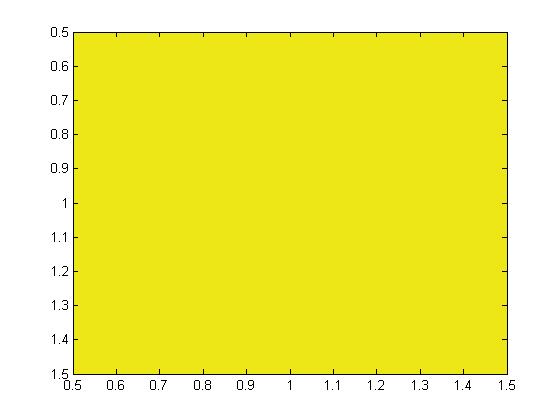
Looks like we found yellow! How about some of the other colors? The left-most bright spot is at about (-68,70). The right-most spot is at about (60,70), and the top-most spot is at about (-4,-47).
lab = [90 -68 70; 90 60 70; 90 -4 -47];
rgb = applycform(lab, makecform('lab2srgb'))
rgb =
0.3737 1.0000 0.2844
1.0000 0.6832 0.3652
0.6637 0.9077 1.0000
image([1 2 3]) colormap(rgb)
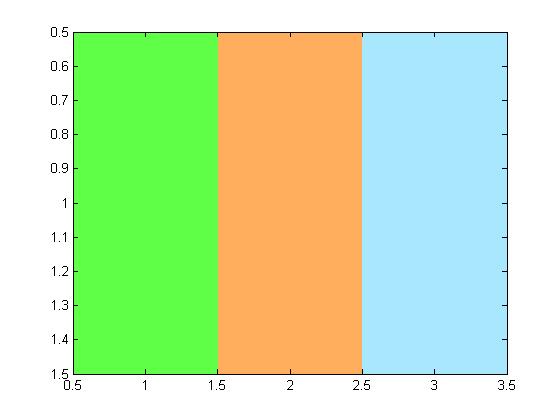
The two colors on the right don't look that much like any of our M&Ms. Maybe I guessed wrong about L*.
lab(:,1) = 50
lab =
50 -68 70
50 60 70
50 -4 -47
rgb = applycform(lab, makecform('lab2srgb'));
image([1 2 3])
colormap(rgb)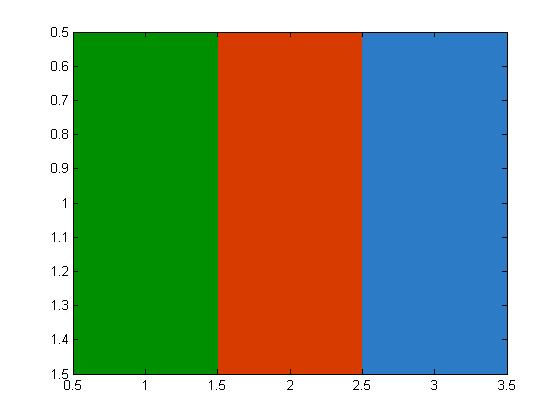
That's better. We found our green, red, and blue M&M colors.
Note added 27-Apr-2021: The following explanation fails to note that many of the colors in the a*-b* plane are actually out of gamut. See the updated discussion of this topic in the 27-Apr-2021 post, "Plotting a* and b* colors."
Here's a crude way to visualize all the colors of the a*-b* plane. We make an "image" containing L*a*b* values and then convert the whole thing to RGB.
[a,b] = meshgrid(-100:100); L = 90*ones(size(a)); lab = cat(3, L, a, b); rgb = applycform(lab, makecform('lab2srgb')); imshow(rgb, 'XData',[-100 100], 'YData', [-100 100]) xlabel('a*') ylabel('b*') axis on
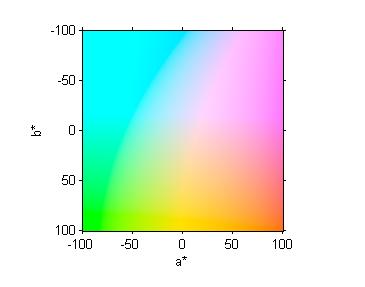
I will continue for a while longer to use this image as an excuse for a pseudorandom walk through some image processing computational and visualization techniques. We've looked at color-space conversion, two-dimensional histograms, and ways to show individual color patches.
I think that next time I'll start to look at segmentation based on color.
In the meantime, Happy New Year everyone!
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。