More on segmenting in a*-b* space
I'm back to looking at M&Ms today. (Previous posts: 17-Dec-2010, 23-Dec-2010, 30-Dec-2010, 11-Jan-2011)
url = 'https://blogs.mathworks.com/images/steve/2010/mms.jpg';
rgb = imread(url);
imshow(rgb)
Last time I showed how I used imfreehand to segment the region in the a*-b* plane corresponding to the green M&Ms.

This time I'll use connected-components labeling and regionprops to segment the image based on all the colors, including the desk background.
I saved the previously computed a*-b* histogram in a MAT-file online; here's how to retrieve and display it.
matfile_url = 'https://blogs.mathworks.com/images/steve/2011/freehand_segment.mat'; temp_matfile = [tempname '.mat']; urlwrite(matfile_url, temp_matfile); s = load(temp_matfile); delete(temp_matfile) H = s.H; imshow(H, [0 1000], 'InitialMagnification', 300, 'XData', [-100 100], ... 'YData', [-100 100]) axis on
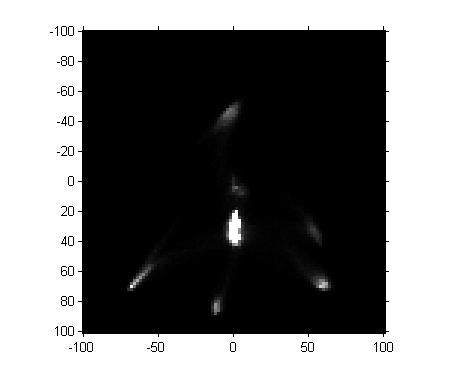
Next, let's threshold the image. (Magic Number Alert! I chose the threshold manually based on visual inspection of pixel values.)
mask = H > 100;
imshow(mask, 'InitialMagnification', 300, 'XData', [-100 100], ... 'YData', [-100 100]) axis on
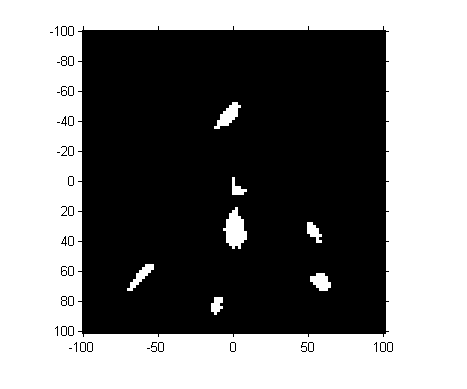
So we've got seven "blobs". Let's measure their centroids.
props = regionprops(mask, s.H, 'Centroid');
props(1)
ans =
Centroid: [20.2143 82.5357]
centers = cat(1, props.Centroid)
centers = 20.2143 82.5357 45.4706 92.2353 49.2973 29.0541 51.6029 67.1765 52.2667 53.4667 77.8000 67.8000 80.1724 84.4483
These centroid values are in the intrinsic pixel coordinates of the image. To convert them to a* and b* values, we have to scale and shift.
ab_centers = 2*centers - 102
ab_centers =
-61.5714 63.0714
-11.0588 82.4706
-3.4054 -43.8919
1.2059 32.3529
2.5333 4.9333
53.6000 33.6000
58.3448 66.8966
a_centers = ab_centers(:,1); b_centers = ab_centers(:,2);
Next question: where are these centers, and what are the regions in the a*-b* plane closest to each one? The voronoi function shows you both.
hold on voronoi(a_centers, b_centers, 'r') hold off
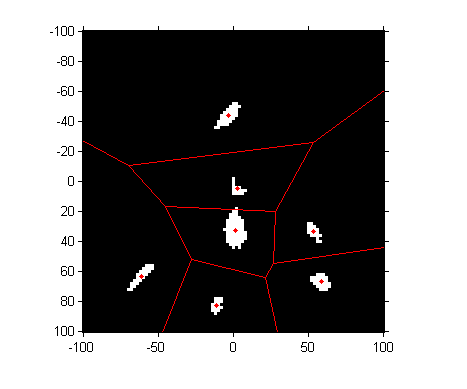
To perform a nearest-neighbor classification of all the pixels, let's compute the Delaunay triangulation, from which we can easily do the nearest-neighbor calculation.
dt = DelaunayTri(a_centers, b_centers)
dt =
DelaunayTri
Properties:
Constraints: []
X: [7x2 double]
Triangulation: [7x3 double]
Compute the a* and b* values of all the pixels:
lab = lab2double(applycform(rgb, makecform('srgb2lab')));
L = lab(:,:,1);
a = lab(:,:,2);
b = lab(:,:,3);For every pixel in the original image, find the closest a*-b* centroid by using the nearestNeighbor function with the Delaunay triangulation.
X = nearestNeighbor(dt, a(:), b(:)); X = reshape(X, size(a));
I would like to make a colormap of the seven colors in our segmentation. We have a* and b* values for each of the colors, but not L* values. We could just make up a constant L* value. Instead, I'll compute the mean L* value for all the pixels closest to the centroid of each of the histogram blobs.
L_mean = zeros(size(a_centers)); for k = 1:numel(L_mean) L_mean(k) = mean(L(X == k)); end
Now we convert the L*a*b* values corresponding to each of our seven colors back to RGB using applycform.
map = applycform([L_mean, a_centers, b_centers], makecform('lab2srgb'))
map =
0.2587 0.8349 0.1934
0.8724 0.8465 0.0271
0.1095 0.4111 0.6803
0.8382 0.7591 0.5286
0.3304 0.2993 0.2751
0.7264 0.2055 0.2008
0.9653 0.3595 0.0690
And finally we can use X and map to display our segmented result as an indexed image.
close all
imshow(X, map)
Not bad!
Unless I have some inspiration between now and next week, I might be ready to let this image go and search for something else to write about.









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.