I recently saw some code that transformed the RGB pixel values of an image into a Px3 matrix, such that each row contained the red, green, and blue color components of a single pixel. Today I want to show that code fragment, explain it, and then demonstrate what I think is the fastest possible to perform that transformation in MATLAB.

I tend to use the peppers sample image a lot, so I'll switch things up and use NGC6543 instead:

RGB = imread('ngc6543a.jpg');
imshow(RGB)

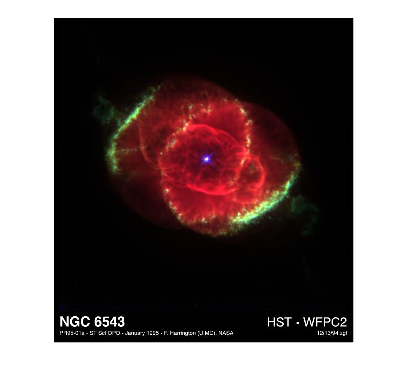
Historical note: This was the first "truecolor" sample image to ship with MATLAB.

RGB is a three-dimensional array:

size(RGB)

ans =

   650   600     3

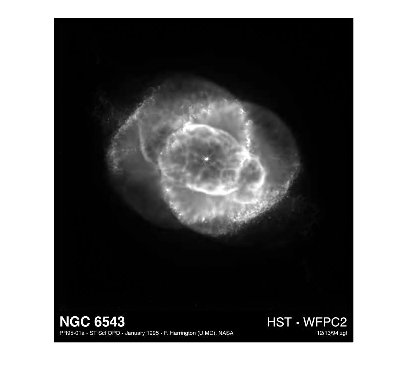
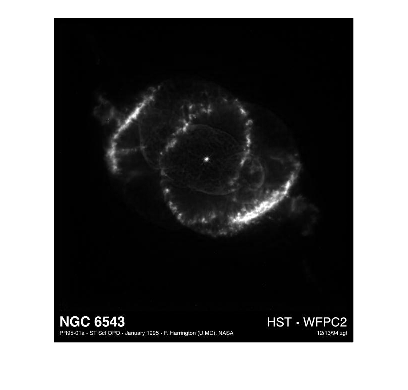
The third dimension, which has length three, contains the red, green, and blue component images. Compare, for example, the red and green component images:

imshow(RGB(:,:,1))

imshow(RGB(:,:,2))

Here is the code that I saw for transforming this array into a Px3 matrix, where each row contains the three color component values of one pixel:

red = RGB(:,:,1);
green = RGB(:,:,2);
blue = RGB(:,:,3);

A = [red(:) green(:) blue(:)];

The first five pixels are along the uppermost left edge of the image, and they are all black:

A(1:5,:)

ans =

  5×3 uint8 matrix

   0   0   0
   0   0   0
   0   0   0
   0   0   0
   0   0   0

The first three lines of code did not give me pause:

red = RGB(:,:,1);
green = RGB(:,:,2);
blue = RGB(:,:,3);

I have written code just like that approximately 2.7183 bazillion times. It was the next line that made me stop and scratch my head for a moment:

A = [red(:) green(:) blue(:)];

Hmm. The array is being split apart into three components, which are then immediately put back together into a matrix. That suggests ... reshape, maybe?

Yes, as it turns out, this can all be done with a call to reshape. And, there is a big advantage to doing so, as I'll explain in a moment. First, the new code:

B = reshape(RGB,[],3);

That line of code says, "MATLAB, reshape the array RGB so that it is Px3, and will you please just go ahead and figure out what P should be to make it work?"

You see in a call to reshape, the number of elements must not change. Here are the number of elements of the array RGB:

numel(RGB)

ans =

     1170000

To reshape that successfully into a matrix with 3 columns, we can compute how many rows there must be:

P = numel(RGB) / 3

P =

      390000

The empty matrix as the second argument to reshape signals to MATLAB to compute that size automatically. That works out just fine:

size(B)

ans =

      390000           3

So, each column of B has 390,000 elements. The first column of B contains the first 390,000 elements (in memory order) of RGB. The second column of B contains the second 390,000 elements of RGB, and similarly for the third column. Because of the way MATLAB arrangements elements in memory, these columns are exactly the elements from the red component, the green component, and the blue component of RGB.

The big advantage of doing it this way is that MATLAB makes no memory copy of data when calling reshape. Because of this optimization, calls to reshape are almost instantaneous.

Let reshape be your friend.

Get the MATLAB code

Published with MATLAB® R2019a