Rubik’s Cube
My recent obsession with cubes in this blog has led me back to Rubik's cube, perhaps the greatest mathematical puzzle of all time.

Contents
Cube Craze
We have been fascinated with the Rubik's cube for almost half a century. People want to solve the puzzle quickly or with as few moves as possible. People also want to recognize the puzzle with a computer vision system and manipulate it with a robotic hand. I am not going to do any of that.
I am interested in the Rubik's cube for several other reasons.
- Illustrate mathematical ideas including rotation matrices and group theory.
- Investigate basic computer science concepts including stacks and queues.
- Discuss computer graphics terms including patches and color.
- Explore MATLAB programming with cell arrays, singleton expansion and unusual subscripts.
Ernő Rubik
In 1974 Ernő Rubik was a professor of architecture at the Budapest College of Applied Arts. Seeking a task for his students, he crafted the first of his now famous puzzles with wood and rubber bands. When it took him a month to unscramble the puzzle, he realized he had something that might be interesting beyond his class. Over 300 million Rubik's cubes have been manufactured since that first prototype. A video from a 2020 New York Times article shows an expert attempting to solve one of the puzzles that are available today. The expert in the video is Ernő Rubik himself.
Pieces
An ingenious spring mechanism holds Rubik's puzzle together while allowing rotation of its faces. An abstract mathematical model of the puzzle need not have springs or other physical constraints. Instead we can use 27 copies of the object described in this blog, arranged in a 3x3x3 grid. Let's use the term piece for these little cubes retain cube for the entire puzzle. Here is one of the individual pieces.
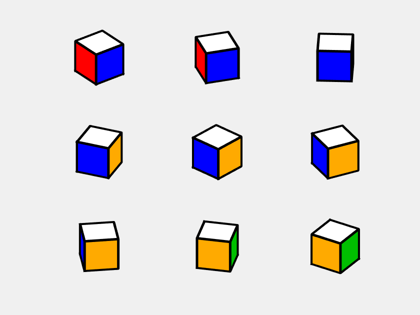
You can see that three of the faces are colored red, white and blue. With the traditional Rubik's cube color scheme, the face opposite the red face is orange and the face opposite the blue one is green. The rotation above is about the z-axis; rotation about other axes reveals that the face opposite the white one is yellow. For a little variety, I sometimes change the color scheme.
Four types
The individual pieces have four types, center, face, edge and corner. Here is what happens when you start with the center piece, add the six pieces at the face centers, then add the twelve edge pieces, and finally add the eight corner pieces. If you follow this blog, you will recognize players from the Menger sponge.
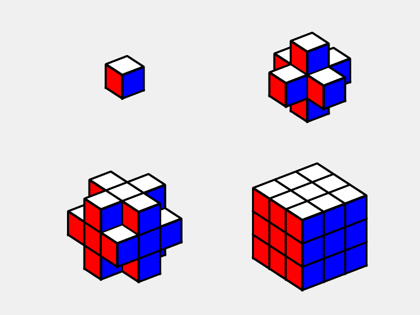
The center piece is never visible and would rotate only if the view point of the entire puzzle were rotated.
There are six pieces at the centers of the six puzzle faces. Each one rotates when its face is rotated but stays in the center of its face.
There are twelve pieces representing the twelve puzzle edges. Each edge piece shows the colors of its faces, red-white, white-blue and so on. There is no blue-green edge piece because the blue and green faces of the puzzle never share a common edge.
There are eight corner pieces, each showing three colors, red-white-blue, white-blue-yellow, and so on. Of the 6x5x4 = 120 possible combinations of six colors, only eight are needed for the corner pieces.
Rubiks_cube
There are dozens of digital Rubik' cubes available on the Web and even a few in MATLAB Central. I am about to contribute one more. Here is a screen shot from that program, which will be featured in a future blog post.









댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.