When the starting point of Newton's method is not close to a zero of the function, the global behavior can appear to be unpredictable. Contour plots of iteration counts to convergence from a region of starting points in the complex plane generate thought-provoking fractal images. Our examples employ the subject of two recent posts, the historic cubic $x^3-2x-5$. ... 続きを読む >>

Use the historic cubic polynomial $x^3 - 2x - 5$ to test a few zero-finding algorithms. ... 続きを読む >>

MATLAB adds capability to search for an interval with a sign change.... 続きを読む >>

Richard Brent's improvements to Dekker's zeroin algorithm, published in 1971, made it faster, safer in floating point arithmetic, and guaranteed not to fail. ... 続きを読む >>

Th. J. Dekker's zeroin algorithm from 1969 is one of my favorite algorithms. An elegant technique combining bisection and the secant method for finding a zero of a function of a real variable, it has become fzero in MATLAB today. This is the first of a three part series.... 続きを読む >>

Augustin (Austin) Dubrulle deserves to be better known in the numerical linear algebra community. His version of the implicit QR algorithm for computing the eigenvalues of a symmetric tridiagonal matrix that was published in a half-page paper in Numerische Mathematik in 1970 is faster than Wilkinson's version published earlier. It is still a core algorithm in MATLAB today. ... 続きを読む >>

This is the third in a multi-part series on the MATLAB random number generators. MATLAB has used variants of George Marsaglia's ziggurat algorithm to generate normally distributed random numbers for almost twenty years. ... 続きを読む >>

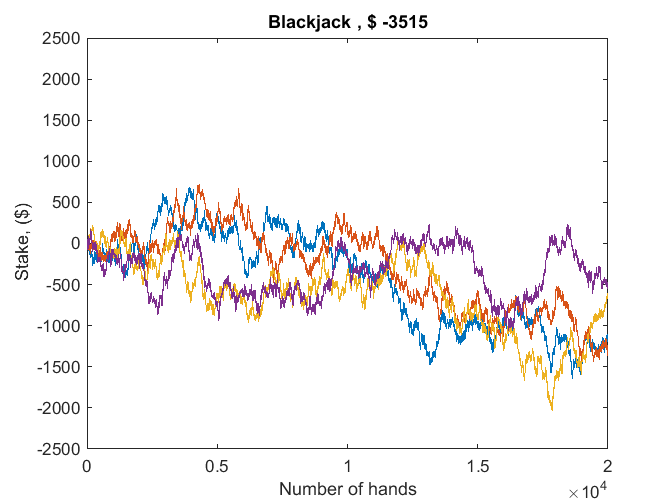
This is the second of a multi-part series about the MATLAB random number generators. If you ask for help rng, you will get lots of information, including the fact that there are three modern generators.... 続きを読む >>

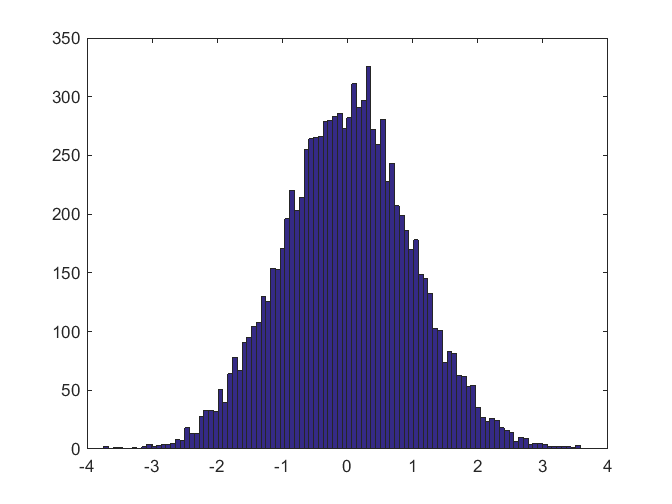
This is the first of a multi-part series about the MATLAB random number generators.... 続きを読む >>

Single and double precision are combined to facilitate a triple precision accumulated inner product.... 続きを読む >>