Parallel Random Number Generators
This is the second of a multi-part series about the MATLAB random number generators. If you ask for help rng, you will get lots of information, including the fact that there are three modern generators.
'twister' Mersenne Twister 'combRecursive' Combined Multiple Recursive 'multFibonacci' Multiplicative Lagged Fibonacci
My previous post was about twister. Today's post is about the other two, 'combRecursive' and 'multFibonacci', which are designed for parallel computing.
Contents
Parallel computing demo
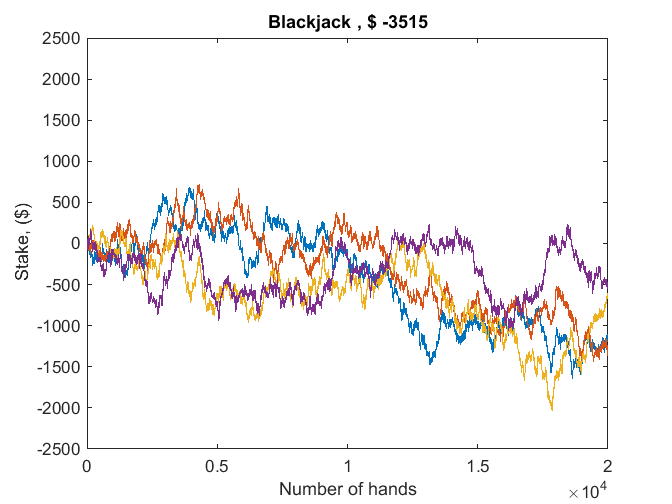
I frequently use the card game Blackjack to demonstrate parallel computing. At the same time I can demonstrate the random number generators. I regard Blackjack as a financial instrument, not unlike the stock of a publicly traded company. Simulating the size of an investment as a function of time is a typical application of the Monte Carlo technique.
Begin by opening a pool of workers.
parpool;
Starting parallel pool (parpool) using the 'local' profile ... connected to 2 workers.
Four players each play twenty thousand hands of Blackjack.
p = 4; n = 20000;
Collect the results in this array.
B = zeros(n,p);
A parallel for loop executes a Blackjack program that knows nothing about parallel computing.
parfor k = 1:p B(:,k) = cumsum(blackjacksim(n)); end
Plot the results.
plot(B) title(['Blackjack , $ ', int2str(sum(B(end,:)))]) xlabel('Number of hands') ylabel('Stake, ($)') axis([0 n -2500 2500])
Parallel streams
The card dealing calls the random number generator. It is essential that the different parallel workers have different, independent streams of random numbers. The default MATLAB generator twister does not offer this feature. Simply starting twister with different seeds on different workers does not provide statistically independent streams. So we turn to the other generators. To see which one is in use here, run a small spmd, "single program, multiple data" block.
spmd r = rng s = r.State' format short x = rand(1,7) end
Lab 1:
r =
Type: 'combRecursive'
Seed: 0
State: [12x1 uint32]
s =
Columns 1 through 6
1720035765 2052922678 1637499698 3048064580 1173461082 2391850890
Columns 7 through 12
1862757735 2368998908 1385613640 1660833332 146924518 3104031825
x =
0.8789 0.6969 0.0409 0.4609 0.7528 0.2871 0.5241
Lab 2:
r =
Type: 'combRecursive'
Seed: 0
State: [12x1 uint32]
s =
Columns 1 through 6
323405913 3817048408 3712601073 1070773748 1552739185 3267875480
Columns 7 through 12
1594297407 2533167732 3377045245 3413340742 2651847732 1248925296
x =
0.1072 0.3194 0.1048 0.6623 0.0878 0.3692 0.8035
We see that we have two workers, that they are both using the combRecursive generator, that they have the same seed, but different states, so they are generating different random numbers.
combRecursive
Also known as mrg32k3a. A 32-bit combined multiple recursive generator (CMRG), due to Pierre L'Ecuyer, at the Universite de Montreal, and his colleagues, described in the papers referenced below. This generator is similar to the CMRG implemented in the RngStreams package. It has a period of $2^{127}$, and supports up to $2^{63}$ parallel streams, via sequence splitting, and $2^{51}$ substreams each of length $2^{76}$. Here is a link to the C source code. combmrg2.c
The state of the backbone generator is a 2-by-3 array S that evolves at each step according to the linear recurrence expressed succinctly in MATLAB by
m1 = 2^32 - 209;
m2 = 2^32 - 22853;
x1 = mod(1403580*S(1,2)-810728*S(1,3),m1);
x2 = mod(527612*S(2,1)-1370589*S(2,3),m2);
S = [x1 S(1,1) S(1,2))
x2 S(2,1) S(2,2)];
A single precision random real u is then produced by
z = mod(x1-x2,m1); if z > 0, u = z/(m1+1); else, u = m1/(m1+1); end
The important feature of this generator is that it is possible to create different initial states for each worker in a parallel pool so that the resulting streams of random numbers are statistically independent.
multFibonacci
Also known as mlfg6331_64. A 64-bit multiplicative lagged Fibonacci generator (MLFG), developed by Michael Mascagni and Ashok Srinivasan at Florida State University. This generator, which has lags $l=63$ and $k=31$, is similar to the MLFG implemented in the SPRNG package. It has a period of approximately $2^{124}$. It supports up to $2^{61}$ parallel streams, via parameterization, and $2^{51}$ substreams each of length $2^{72}$.
The state of this generator is a length 63 vector of 64-bit integers S. The recurrence relation is
$$ x_n = x_{n-k} \times x_{n-l} (mod 2^{64}) $$
Each random double precision value is created using one 64-bit integer from the generator; the possible values are all multiples of $2^{-53}$ strictly within the interval (0,1).
Again, the important feature of this generator is that it is possible to create different initial states for each worker in a parallel pool so that the resulting streams of random numbers are statistically independent.
Which one?
Which one should you use? Most of the time, stick with the default and you'll be OK. You will get 'twister' in serial computations and 'combRecursive' on the workers in a parallel pool. You can use
rng('shuffle')at the beginning of a session if you want different sequences of random numbers in different sessions. Otherwise, don't worry about setting the generator or the seed.
If you want to experiment, you can use rng to try different generators and different starting seeds on your computation. If you find a problem where it makes a significant difference, please let us know.
Thanks
Thanks again to Peter Perkins.
References
Pierre L'Ecuyer, R. Simard, E. J. Chen, and W. D. Kelton. "An Objected-Oriented Random-Number Package with Many Long Streams and Substreams." Operations Research, 50(6):1073-1075. 2002. <http://www.iro.umontreal.ca/~lecuyer/myftp/papers/streams00.pdf>
Pierre L'Ecuyer. "Good Parameters and Implementations for Combined Multiple Recursive Random Number Generators." Operations Research 47(1):159-164. 1999. <http://dx.doi.org/10.1287/opre.47.1.159>
Michael Mascagni and Ashok Srinivasan. "Parameterizing Parallel Multiplicative Lagged-Fibonacci Generators." Parallel Computing, 30: 899-916. 2004. <http://www.cs.fsu.edu/~asriniva/papers/mlfg.ps>
Michael Mascagni and Ashok Srinivasan. "SPRNG: A Scalable Library for Pseudorandom Number Generation." ACM Transactions on Mathematical Software, Vol 26 436-461. 2000. <http://www.cs.fsu.edu/~asriniva/papers/sprngacm.ps>







コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。