Football Squares Updated for Superbowl LIII
I wrote about Football Squares a long time ago. In light of the upcoming Superbowl, a few people have asked me to brush up my code. As a bonus, it’s been so long since the last time I did this that I can show off some new MATLAB functionality. Here goes…
The game
Is this game is popular with other sports in other countries? I have no idea. But it’s a simple way to let a group of people wager on the outcome of a game.
First you make a 10-by-10 grid. Each square in the grid corresponds to a pair of one-digit numbers. These one-digit numbers, in turn, correspond to the last digit in the final score of one of the two teams. Before the game, everyone buys one or more squares until they’ve all been sold. Now, if the Alligators (team A) go on to defeat the Buckaroos (team B) by a score of 17 to 10, then the owner of the square at location (7,0) would be the winner.
As you can imagine, some score pairs are much more likely than others. For this reason, you buy the squares before the numbered labels are applied. In other words, it’s dumb luck whether or not you win. The best kind of beer-and-ballgame wager!
I’ll spell out how it works in this Live Script.
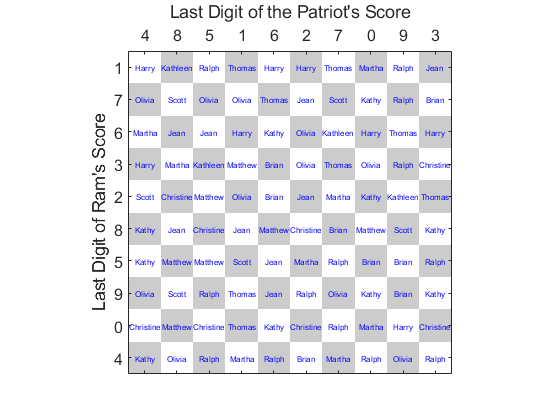
Draw the grid
a = invhilb(10)<0;
Why INVHILB? See this Cody problem.
tick = 0:9; imagesc(tick,tick,a) colormap([1; 0.8]*[1 1 1]) set(gca, ... 'FontSize',12, ... 'XAxisLocation','top', ... 'XTick',tick, ... 'YTick',tick, ... 'XTickLabel','?', ... 'YTickLabel','?') axis square xlabel("Last Digit of the Patriots Score") ylabel("Last Digit of Rams Score")

So you can see that we don’t actually know which numbers will correspond to each square.
Pick the squares
We’ll use a random name generator from the web to come up with a list of players. WEBREAD is a nifty command: it’s automatically turning the returned JSON into a structure for me.
url = 'https://uinames.com/api/?amount=12®ion=United%20States';
names = webread(url);
These are all the people coming to your party. Don’t worry, they’re a lot of fun.
allNames = string({names.name});
disp(allNames.join(', '))
Thomas, Kathleen, Matthew, Jean, Christine, Kathy, Martha, Scott, Brian, Olivia, Harry, Ralph
Now we’ll simulate people buying up the squares. Say they’re paying one dollar for each square, for a nice $100 jackpot.
groupSize = 12; nameIndexGrid = randi(groupSize,[10 10]); for i = 1:numel(a) [row,col] = ind2sub([10,10],i); text(col-1,row-1,allNames(nameIndexGrid(col,row)),... 'FontSize', 6, ... 'Color','blue', ... 'HorizontalAlignment','center'); end

Assign the score digits
Now that the squares have all been purchased, it’s time to assign the actual digits to the grid. This is a perfect task for RANDPERM.
xLabels = randperm(10)-1; yLabels = randperm(10)-1; set(gca, ... 'XTickLabel',string(xLabels), ... 'YTickLabel',string(yLabels))
What are the last digits of the final score?
Now I’m going to come up with a fake final score. Even though this is a simulation, I won’t reveal who wins. No point in stirring up trouble! We’re based in Boston, so we’re fond of the Patriots. But believe me, we know that’s not a …ahem… widely held opinion across the country.
patriotsFinalScore = randi(30); ramsFinalScore = randi(30);
Let’s make a little anonymous function here, because anonymous functions are cool.
getLastDigit = @(score) score - 10*(floor(score/10));
What are the last digits in the score?
patriotsLastDigit = getLastDigit(patriotsFinalScore)
patriotsLastDigit = 6
ramsLastDigit = getLastDigit(ramsFinalScore)
ramsLastDigit = 6
ix1 = find(patriotsLastDigit==xLabels); ix2 = find(ramsLastDigit==yLabels); set(findobj('Type','text'),'Color',0.6*[1 1 1]) patch(ix1-1+[0 1 1 0 0]-0.5,ix2-1+[0 0 1 1 0]-0.5,[1 0.7 0.7],'EdgeColor','none') text(ix1-1,ix2-1,allNames(nameIndexGrid(ix1,ix2))+" wins!",... 'FontSize',18, ... 'FontWeight','bold', ... 'Color','red', ... 'HorizontalAlignment','center');









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.