Solving Sudoku with MATLAB
Today's guest article is by Wesley Hamilton, a STEM Outreach engineer here at MathWorks. Wesley's roles involve popularizing the use of MATLAB and Simulink for younger folk, especially towards mathematical topics, and this blog is an accompanying piece to a workshop being run by the National Museum of Math in New York City.
Sudoku is a popular puzzle in which puzzlers fill in a 9x9 grid with the digits 1-9 such that a number of conditions are met: each 3x3 subgrid, row, and column must contain all digits. While Sudoku is usually referred to as a logic puzzle, it is actually possible to recast these puzzles as a (mathematical) constrainted optimization problem, wherein the optimal solution gets interpreted as the inputs for a completed Sudoku puzzle. What's crazy about this formulation though is that the function we optimize will be the zero function, so that any input is optimal; all of the legwork is in satisfying the optimization problem's constraints. Interested? Read on to learn more!
The presentation and code in this blog are adapted from a workshop developed by Dr. Tim Chartier, based on code developed in collaboration with Dr. Amy Langville of the College of Charleston and her students.
Table of Contents
Rules and History of Sudoku
Solving Sudoku Puzzles, part 1
Linear Programming
Sudoku as a Linear Program
Box constraints
Row constraints
Column constraints
Subgrid constraints
Solving Sudoku Puzzles, part 2
Ordering of decision variables
Box constraints
Row constraints
Column constraints
Subgrid constraints
The givens
Further directions
Just the code
Solving Sudoku Puzzles, part 1
Linear Programming
Sudoku as a Linear Program
Box constraints
Row constraints
Column constraints
Subgrid constraints
Solving Sudoku Puzzles, part 2
Ordering of decision variables
Box constraints
Row constraints
Column constraints
Subgrid constraints
The givens
Further directions
Just the code
Rules and History of Sudoku
The classic version of Sudoku most people are familiar with consists of a 9x9 grid divided into nine 3x3 subgrids. The grid will start with some boxes filled in with the digits 1-9, and the goal of the puzzle is to fill in each box with one of the 9 digits in a way that the following three conditions are satisfied:
- Every row of the grid contains each of the digits 1-9, and each digit only appears once,
- Every column of the grid contains each of the digits 1-9, and each digit only appears once,
- Every 3x3 subgrid contains each of the digits 1-9, and each digit only appears once.
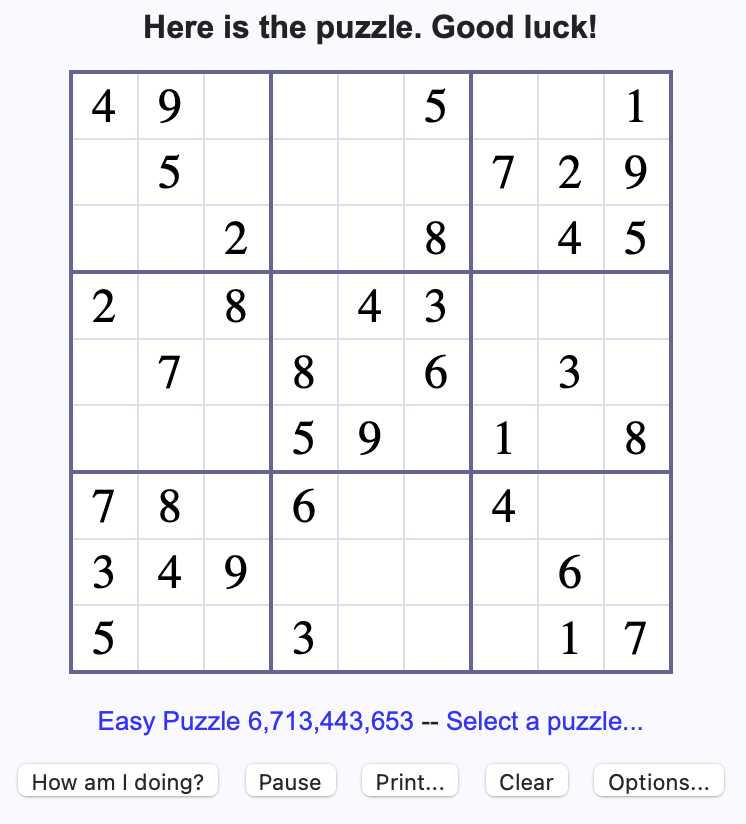
Here is an example of a 9x9 Sudoku puzzle, retrieved from websudoku.com on May 3, 2023.
One variation of the puzzle is the 4x4 version, in which a 4x4 grid is split into four 2x2 subgrids and the three conditions are modified so that only the digits 1-4 are used. This version is often used as an easier version than the 9x9, and makes visualizing what happens in the computational side of things a bit more tractable as well.
Here is an example of a 4x4 Sudoku puzzle, generated by Dr. Tim Chartier, MoMath's 2022–2023 Distinguished Visiting Professor for the Public Dissemination of Mathematics.

Sudoku was popularized in Japan in the late 1980s, before grabbing worldwide attention in the early 2000s. Unbeknownst to many, very early versions of Sudoku appeared in France in the late 1800s as puzzle-variations of magic squares; see the Wikipedia page and its references for more information.
The next section walks through the basics of solving Sudoku puzzles. If you're already very familiar with Sudoku, feel free to skip down to the text right after the completed 4x4 puzzle.
Solving Sudoku Puzzles, part 1
So how does one solve a Sudoku puzzle? In practice, we iteratively apply the three conditions to identify which numbers go in which boxes until all boxes are filled in. In harder puzzles we may be forced to make a choice between two equally likely entries; in these situations we'll often try writing in one of the options and seeing what other numbers can get filled in based on that, and then either run into a contradiction, or solve the board.
Let's see this process in action with Tim's 4x4 puzzle. For clarity, the three conditions we'll be iteratively checking are:
- Every row of the grid contains each of the digits 1-4, and each digit only appears once,
- Every column of the grid contains each of the digits 1-4, and each digit only appears once,
- Every 2x2 subgrid contains each of the digits 1-4, and each digit only appears once.
First we'll focus on the upper-right 2x2 subgrid and identify where we may be able to fill in a number, in either the red circle or the blue square.

Applying condition 3., we know that the digits in these empty grid boxes have to be 2 and 3. So which digit goes where? By condition 2., each column of the grid can only contain each digit exactly once, and the fourth column (containing the blue square) already contains a 2, so it is not possible to write the digit 2 in the blue square (similarly, by condition 1. the row with the blue square already has the digit 2 somewhere in the row). Thus, the digit 2 goes in the square with the red circle.
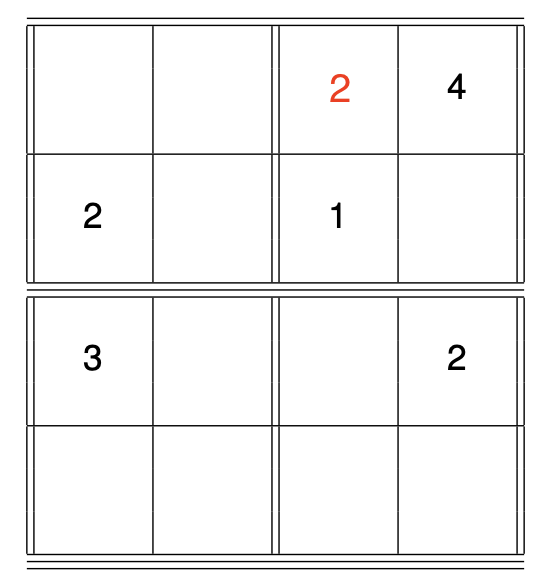
Applying condition 3. to the same subgrid, we conclude the remaining grid box must contain the digit 3.

Continuing in this way we'll eventually be able to fill in every box; for example, the next move might be writing in the digit 4 in the only remaining box in the second row. Feel free to try solving this 4x4 on your own, and check your solution against ours:

Awesome! But what if we want to have MATLAB solve the puzzle for us? An initial approach might be to code (in some way) these three constraints and have our computer iterate through each row, column, and subgrid writing in digits one-by-one. What happens if there are two digits that might work in a grid box? Are there other logical steps that might occur in a harder puzzle that we can't anticipate?
Instead of taking this approach, we'll take a very different, and possibly cleverer, approach making use of some deep and powerful computational mathematics known as Linear Programming.
Linear Programming
Linear programming is, simply put, an optimization problem in which the objective function and constraints are all linear. Let's break down what each of these pieces mean:
- an optimization problem is a problem in which one seeks the maximum (or minimum) of an objective function, i.e. find a value for x that maximizes a given function $ f(x) $;
- an objective function is the function we want to maximize or minimize. We could just call it a function, but often in optimization problems multiple functions come in to play, including functions that add constraints to the problem, in addition to the function we're optimizing;
- a linear objective function is an objective function that is linear, i.e. takes the form $ f(x) = a_1 x_1 + \cdots + a_n x_n $, for a vector $ x = \pmatrix{x_1 \cr \vdots \cr x_n} $. Writing $ a = \pmatrix{a_1 \cr \vdots \cr a_n} $, this function can also be expressed $ f(x) = a^t x $, where the t superscript means we're taking the matrix transpose of a vector.
- a constraint is a rule for which values of x are feasible, i.e. x must be non-negative, or if x is a vector then all of the components of x must be non-negative;
- a linear constraint is a constraint that's written in the form of a linear equation. For example, if we're working with a vector $ x = \pmatrix{x_1 \cr x_2 \cr x_3} $, then a linear constraint might look like $ x_1 - x_2 + 3 x_3 \leq 0 $. If we write $ b=\pmatrix{1 \cr -1 \cr 3} $, then this linear constraint can also be written $ b^t x \leq 0 $, where the t superscript means we're taking the matrix transpose of a vector.
Linear constraints can actually come in two forms: linear inequalities ($ Ax\leq b $) and linear equalities ($ A_{eq} x = b_{eq} $). Both kinds of constraints The kinds of linear programs we'll work with here can all be expressed in the following form:
find a vector x that maximizes $ f(x) = a^t x $ subject to $ Ax \leq b $, $ A_{eq} x = b_{eq} $, and $ x\geq 0 $,
where $ a, b, b_{eq} $ are given vectors, and $ A, A_{eq} $ are given matrices encoding the linear constraints. Note that if $ x = \pmatrix{x_1 \cr \vdots \cr x_n} $, then the notation $ x\geq 0 $ means $ x_i \geq 0 $ for $ i=1, ..., n $. The components $ x_i $ of the vector x are often called decision variables, since these are the values the linear program needs to decide, or find values for.
In this post we'll be using MATLAB's intlinprog function, which you can treat as a black box linear program solver that finds integer solutions to a linear program. This solver automatically selects which algorithm to use and works to find a solution, so the only work we have to do is write down the linear program in a way it can understand. We'll do that next.
Keep in mind that we're using a matrix multiplication formulation to express the constraints. For background on matrix multiplication and basic linear algebra concepts, check out our interactive courseware module on Matrix Methods of Linear Algebra.
Sudoku as a Linear Program
To set up a Sudoku puzzle as a linear program, we need to identify a few things:
- What are the variables that we're solving for?
- What are the constraints we want to impose?
- What is the function we want to maximize?
Why not identify the function before the constraints? Well, turns out we don't actually care what the function is, which will be clear by the end of this section.
So what should the variables be? For a 4x4 grid we have 16 total boxes to fill in, and an initial approach might be to use variables $ x_1, ..., x_{16} $ where each $ x_i $ should take a value between 1 and 4. While reasonable, there's actually a computationally easier approach.
Instead of using the variables to tell us which digit is in each box, let's use variables to tell us whether or not a digit is in a box. By this we mean using variables $ x_{ijk} $, where the pair $ (i,j) $ tells us which box we're looking at, and k specifies which digit we care about. If $ x_{ijk} = 0 $, then digit k should not be written in box $ (i,j) $, while if $ x_{ijk} = 1 $, then digit k belongs in box $ (i,j) $.
As an example, consider the 4x4 grid we considered earlier (with some of the box indeces added in the top-left corners for clarity):

To number the grid boxes, $ (1,1) $ will be the top-left box, $ (2,1) $ will be the box beneath it, and $ (1,2) $ will be the box to the right of $ (1,1) $. In other words, the first index i in $ (i,j) $ counts how many rows down we go, and the index j counts how many columns to the right we go.
So with this notation, we have the digit 4 in the $ (1,4) $ box, the digit 1 in the $ (2,3) $ box, and the digit 2 in the $ (3,4) $ box at the start (among others). In particular, the digits $ 1,2,3 $ do not appear in the $ (1,4) $ box. Using our variables to encode this information, we'd have $ x_{1,4,4}=1 $ and $ x_{1,4,1} = x_{1,4,2} = x_{1,4,3} = 0 $. At the start of the puzzle we did not know which digit went in the $ (1,3) $ box, so at the start $ x_{1,3,k} $ is not specified for $ k=1,...,4 $. Using the rules of Sudoku, we identified that a 2 belongs in that box, so by using the constraints we concluded that $ x_{1,3,2} = 1 $ and $ x_{1,3,1}=x_{1,3,3} = x_{1,3,4} = 0 $. Now that we have our variables specified, we're in a position to specify the constraints.
So how do we encode the Sudoku constraints into this framework? Keep in mind there are three constraints from the original puzzle which we'll need to encode in turn. There's actually a fourth constraint we need to encode, as discussed just above, in which each box can only have a single digit written in it.
Box constraints
The first constraint we need to encode is that each box can only have one digit written in it. So, for the $ (i,j) $ box, as soon as the digit 1 is written in it (for example), we get $ x_{i,j,1} = 1 $ and $ x_{i,j,2} = x_{i,j,3} = x_{i,j,4} = 0 $. The trick here is that each variable should take the value of either 0 or 1 (and nothing else), so if we sum them up and set the sum equal to 1, that ensures only one of the variables can take the value 1. Written out explicitly, for each of the boxes $ (i,j) $ we require:
$ x_{i,j,1} + x_{i,j,2} + x_{i,j,3} + x_{i,j,4} = 1 $.
Row constraints
The first of the puzzle constraints is that each row of the grid has each of the digits, and that each digit only appears once. Since we're looking at the rows, we're going to be focusing on sets of variables $ x_{i,1,k}, x_{i,2,k}, x_{i,3,k}, x_{i,4,k} $ for $ i = 1,...,4 $ and $ k=1,...,4 $. The trick here is the same as above, in that each variable should take the value of either 0 or 1 (and nothing else), so if we sum them up then, in a solved puzzle, we should get exactly 1:
$ x_{i,1,k} + x_{i,2,k} + x_{i,3,k} + x_{i,4,k} = 1 $.
As soon as one of the $ x_{i,j,k} $ takes the value 1, the rest are forced to be 0. This ensures that, in the ith row, the digit k only appears once. This constraint should hold for every possible row i and possible digit k.
Column constraints
The column constraint is set up exactly the same way as the row constraint, except here we're summing over the row indeces instead of the column indeces:
$ x_{1,j,k} + x_{2,j,k} + x_{3,j,k} + x_{4,j,k} = 1 $,
and this equality should hold for every possible column j and digit k.
Subgrid constraints
The last of the Sudoku puzzle constraints to implement is the subgrid rule, in which each of the four digits is present in each of the 2x2 subgrids. As a specific example to guide our work, consider the subgrid in the top-left consisting of the boxes $ (1,1), (1,2), (2,1), (2,2) $. The subgrid constraint specifies that each digit k appears just once among these four boxes, so we'll actually have four constraints for this subgrid:
$ x_{1,1,k} + x_{1,2,k} + x_{2,1,k} + x_{2,2,k} = 1 $, $ k=1,...,4 $.
There are four of these subgrids though, so we also need to incorporate those constraints:
$ x_{1,3,k} + x_{1,4,k} + x_{2,3,k} + x_{2,4,k} = 1 $, $ k=1,...,4 $,
$ x_{3,1,k} + x_{3,2,k} + x_{4,1,k} + x_{4,2,k} = 1 $, $ k=1,...,4 $,
$ x_{3,3,k} + x_{3,4,k} + x_{4,3,k} + x_{4,4,k} = 1 $, $ k=1,...,4 $.
That's a lot! Good thing we don't have to work with all of these equations by hand and have MATLAB to do all the heavy lifting for us!
The last thing we need to do is specify what our objective function is, the thing we're actually minimizing. The thing is, though, we've already encoded everything we want to keep track of through the variables and constraints, so there isn't any need for a specific function. This means that, for our purposes, we're free to set the function to be $ f(x) = 0 $. In this case, any vector x maximizes the function, so all of the work goes into finding a vector x that satisfies the constraints. If this still seems weird, you're not alone; if it helps, you're welcome to just have faith that we'll get a solution using this weird function, that's perfectly fine.
To summarize our work in this section, we're solving the following linear program:
find a vector $ x = \pmatrix{x_{1,1,1}\cr x_{1,1,2}\cr \vdots \cr x_{4,4,4}} $ that maximizes the function $ f(x) = 0 $, subject to the constraints
- $ x_{i,j,1} + x_{i,j,2} + x_{i,j,3} + x_{i,j,4} = 1 $ for $ i = 1,...,4 $ and $ j=1,...,4 $, (box constraint)
- $ x_{i,1,k} + x_{i,2,k} + x_{i,3,k} + x_{i,4,k} = 1 $ for $ i = 1,...,4 $ and $ k=1,...,4 $, (row constraint)
- $ x_{1,j,k} + x_{2,j,k} + x_{3,j,k} + x_{4,j,k} = 1 $ for $ j = 1,...,4 $ and $ k=1,...,4 $, (column constraint)
- $ x_{1,1,k} + x_{1,2,k} + x_{2,1,k} + x_{2,2,k} = 1 $ for $ k=1,...,4 $, (top-left subgrid constraint)
- $ x_{1,3,k} + x_{1,4,k} + x_{2,3,k} + x_{2,4,k} = 1 $ for $ k=1,...,4 $, (top-right subgrid constraint)
- $ x_{3,1,k} + x_{3,2,k} + x_{4,1,k} + x_{4,2,k} = 1 $ for $ k=1,...,4 $, (bottom-left subgrid constraint)
- $ x_{3,3,k} + x_{3,4,k} + x_{4,3,k} + x_{4,4,k} = 1 $ for $ k=1,...,4 $. (bottom-right subgrid constraint)
Note that all of this work was just for the 4x4 version of Sudoku; how would we modify everything for the original 9x9 version? Take a minute to think about it, and then read on for a solution... Afterwards we'll implement everything in MATLAB and actually solve some puzzles.
For the 9x9 version, the straightforward changes are that the sums should include 9 terms everywhere, and the indeces $ i,j,k $ should each range from 1 to 9 everywhere. The more-involved modification is that there will be nine subgrid constraints instead of four, since the 9x9 grid contains nine 3x3 subgrids. The top-left 3x3 subgrid will have the constraint
$ x_{1,1,k} + x_{1,2,k} + x_{1,3,k} + x_{2,1,k} + x_{2,2,k} + x_{2,3,k} + x_{3,1,k} + x_{3,2,k} + x_{3,3,k} = 1 $, for $ k = 1, ..., 9 $.
The other subgrid constraints can be written out in a similar (slightly cumbersome) way.
Solving Sudoku Puzzles, part 2
In this section, we'll encode the constraints we described above and actually solve a Sudoku puzzle using linear programming.
There's one other set of constraints that we need to impose, that are independent of our framework and the rules of Sudoku. Remember that a Sudoku puzzle starts with some of the grid boxes filled in, which we can specify by a matrix G specifying the row number, column number, and digit of each of the initial entries. As a concrete example, for our 4x4 example we have $ G = \pmatrix{1 & 4 & 4 \cr 2 & 1 & 2\cr 2 & 3 & 1\cr 3 & 1 & 3 \cr 3 & 4 & 2} $; the first row is $ (1\, 4\, 4) $ since we start with the digit 4 in the first row and fourth column, etc.
The first thing to do is specify the size of the Sudoku grid where working with:
n=4; % for 4 by 4 sudoku problem
%n=9; % for 9 by 9 sudoku problem
Ordering of decision variables
Keep in mind that the vector of variables, specifying which digits appear where in the grid, will have $ n^3 $ entries: $ n\times n $ entries corresponding to each box in the grid, and another n for the n possible digits. One thing we need to be careful about is what order our decision variables appear in our vector. Three (plus one) reasonable options are:
- Order the variables by incrementing the digit index first, then the column index, then the row index: $ x_{1,1,1}, x_{1,1,2}, ..., x_{1,1,4}, x_{1,2,1}, x_{1,2,2}, ... $ This enumeration will list all the digit design variables first before going to a new box.
- Order the variables by incrementing the row index first, then the column index, then the digit index: $ x_{1,1,1}, x_{2,1,1}, ..., x_{4,1,1}, x_{1,2,1}, x_{2,2,1}, ... $ This enumeration will iterate through the entire grid by going down columns then across rows, before increment the digit index and iterating through again.
- Order the variables by incrementing the column index first, then the row index, then the digit index: $ x_{1,1,1}, x_{1,2,1}, ..., x_{1,4,1}, x_{2,1,1}, x_{2,2,1}, ... $ This is similar to the previous possible enumeration, except we traverse the grid along rows first, then along columns, then along digits.
- Order the variables randomly.
The fourth option isn't actually reasonable, since you'll have significantly more bookkeeping to manage (it is, technically, possible to implement though!). Here we'll take option two, so that every set of $ n^2 $ components of the decision vector x correspond to the same digit enumerated along columns and then rows.
Namely, for our implementation here, x(1) tells us whether or not digit 1 is in the $ (1,1) $ box, x(n^2+1) tells us if the digit 2 is in the $ (1,1) $ box, etc. Likewise, x(2) tells us if the digit 1 is in the $ (2,1) $ box, x(3) tells us if the digit 1 is in the $ (3,1) $ box, x(n^2+2) tells us if the digit 2 is in the $ (2,1) $ box, etc.
Extra Challenge: implement this Sudoku solver using the other two (reasonable) methods of ordering the design variables. Extra bonus points for implementing the random ordering approach.
Next let's encode the constraints as a matrix $ A_{eq} $, so that in our linear program we'll have $ A_{eq} x = b $ as our constraint. The matrix $ A_{eq} $ should be a $ C\times n^3 $ matrix, where C is the number of constraints. The vector b will be a vector of 1s, being the right-hand side of each of our constraints.
What is C in this case? The constraints we identified are:
- for each of the $ n^2 $ grid boxes we have a single constraint, totalling $ n^2 $ constraints,
- for each of the n rows, and each of the n digits, we have a constraint, totalling $ n^2 $ constraints,
- for each of the n columns, and each of the n digits, we have a constraint, totalling $ n^2 $ constraints,
- for each of the n subgrids, we have n constraints telling us each digit must appear in that subgrid, totalling $ n^2 $ constraints,
- we start with $ |G| = \# $of rows of G entries already filled in, totalling $ |G| $ constraints.
Summing these numbers up, we get $ C = 4n^2 + G $. In our approach, we'll define $ A_{eq} $ with $ C = 4n^2 $ first and fill in the first four constraints in the above bulleted list. Once finished, we'll add $ |G| $ more rows to $ A_{eq} $ and incorporate the givens. So let's start by initializing $ A_{eq} $:
Aeq=zeros(4*n^2, n^3);
Here's a sketch of the matrix we'll be filling in during the rest of this section:

At the top we've indicated how the decision variables are ordered: the first $ n^2 $ columns correspond to whether or not digit 1 is written in the boxes $ (1,1), (2,1), ..., (n,n) $, the next $ n^2 $ columns correspond to digit 2, and so on, exactly as we specified when we decided to use option 2 for ordering above. The rows are split based on the constraints we're encoding as well as the given entries of the initial Sudoku puzzle.
In the next few subsections we'll iterate through this matrix and write-in each of constraints. The subsections showcase what the matrix will look like (i.e. where the 0's and 1's go), before displaying the MATLAB code that accomplishes this (with plenty of comments).
Box constraints

%% Fill in Aeq for the n^2 constraints requiring that each element
% of the matrix must contain an integer 1:n
for i=1:n % for each row (of the Sudoku grid)
for j=1:n % for each column (of the Sudoku grid)
for k=1:n % increment through each digit
% the (i,j) grid box is associated to row (i-1)*n+j of A_eq
% incrementing the digit k comes with n^2 entries along the array
% though the box index (i,j) stays the same as we incorporate all
% digits
Aeq((i-1)*n+j,(i-1)*n+j + (k-1)*n^2)=1;
end
end
end
% if we had ordered the design variables so that we increment through
% digits first, we could replace this code with
%
% for i=1:n^2
% Aeq(i,(i-1)*n+1:i*n)=ones(1,n);
% end
Row constraints

%% Fill in Aeq for the n^2 constraints requiring that each row
% can have only 1 of each integer 1:n
for k=1:n % for each digit
for i=1:n % fix the row of the Sudoku grid
for j=1:n % increment the column indeces we're summing up
% note that we've already added the n^2 box constraints
% so updating A_eq starts at the n^2 row
Aeq(n^2+i+(k-1)*n,1+(i-1)+(j-1)*n+(k-1)*n^2)=1;
end
end
end
% if we had ordered the design variables so that we increment through
% rows first, we could replace this code with
%
% for i=1:n^2
% Aeq(n^2+i,(i-1)*n+1:i*n)=ones(1,n);
% end
Column constraints

%% Fill in Aeq for the n^2 constraints requiring that each column
% can have only 1 of each integer 1:n
for i=1:n^2 % quick trick since the column constraints correspond to rows of adjacent 1s
% we've added the n^2 box constraints and n^2 row constraints
% so these constraints start on row 2*n^2
% since our variable indexing goes along columns first,
% when incorporating these constraints
Aeq(2*n^2 + i,(i-1)*n+1:i*n)=ones(1,n);
end
Subgrid constraints

%% Fill in Aeq for the n^2 constraints requiring that each submatrix
% can have only 1 of each integer 1:n
% note that n is a square, so sqrt(n) is an integer
% m and l are indeces for the subgrids - m=1, l=1 is the top-left subgrid
for m=1:sqrt(n)
for l=1:sqrt(n) % for the (m,l) subgrid
for j=1:n
for k=1:sqrt(n)
% added n^2 box, n^2 row, and n^2 column constraints
% the subgrid constraints should be added starting at row 3*n^2
Aeq(3*n^2+(m-1)*sqrt(n)*n+(l-1)*n+j,(j-1)*n^2+(l-1)*sqrt(n)+...
(m-1)*sqrt(n)*n+(k-1)*n+1:...
(j-1)*n^2+(l-1)*sqrt(n)+(m-1)*sqrt(n)*n+(k-1)*n+sqrt(n))=1;
end
end
end
end
The givens
Next, we need to incorporate the information that some of the entries are already filled in. We'll do this by specifying the givens in the form of the matrix mentioned at the start of this section, and then writing this information into $ A_{eq} $ in newly added rows below the information we've already incorporated.
For this example, we'll use the same matrix G for our favourite 4x4 example:
% If any values of the Sudoku matrix are given, add these as
% constraints
% Enter each given value in matrix as triplet (row, col, integer)
% Example for 4-by-4 sudoku
Givens=[1 4 4;
2 1 2;
2 3 1;
3 1 3;
3 4 2];
With this matrix specified, let's now append rows to $ A_{eq} $ and incorporate these constraints specifying our given digits:
% turn these given elements into their appropriate position in the x vector
% of decision variables.
g=size(Givens,1);
for i=1:g % for each of the givens
% we've added in 4*n^2 constraints already, so the first of the givens
% should be added at row 4*n^2 + 1, etc.
% the column entry to write the given constraint is at
% rowId + colId*n + digitId*n^2
% based on how we've organized the decision variables
Aeq(4*n^2+i,Givens(i,1)+(Givens(i,2)-1)*n+(Givens(i,3)-1)*n^2)=1;
end
This concludes writing out $ A_{eq} $. The final matrix should resemble this sketch:

Note the 1 at the matrix element corresponding to the given $ (2,1,2) $.
Since all of the constraints are set-up to equal 1, the vector b in $ A_{eq}x = b $ should be a vector of 1s:
beq=ones(4*n^2+g,1);
With the variables and constraints in place, we're almost ready to have MATLAB generate our solution. Looking at the documentation for intlinprog, we need to explicitly specify some other pieces:
- intcon, or the variables in x that should be integers. We want all of the components of x to be integers, so this should be the array 1:numVariables,
- numVariables, or the length of the variable x ($ n^3 $ in this case),
- lb, the vector of lower bounds for each of the variables. Since each $ x_{ijk} $ is 0 or 1, lb will be a vector of 0s,
- ub, the vector of upper bounds for each of the variables. Since each $ x_{ijk} $ is 0 or 1, ub will be a vector of 1s.
Let's go ahead and specify each of these variables:
%% run matlab's "intlinprog" command
numVariables = size(Aeq,2);
intcon = 1:numVariables;
lb = zeros(1,numVariables);
ub = ones(1,numVariables);
With everything in place, let's generate a solution to our 4x4 puzzle.
[x,fval,exitflag,output]=intlinprog(zeros(n^3,1),intcon,[],[],Aeq,beq,lb,ub);
% note the two arguments of []
% these inputs correspond to inequality constraints
% since we're not using inequality constraints, we leave these inputs empty
exitflag;
output;
x
For our 4x4 example, x is a vector with $ 4^3 = 64 $ entries, each of which is 0 or 1. While this is a solution to the linear program, it's not yet helpful for our purposes; what would be nice is if we could convert this vector into a grid of digits 1 to 4, corresponding to a Sudoku solution. Let's do that now and see the result:
%% turn matlab's outputed solution vector x into sudoku terms
S=zeros(n,n); %initialize the grid of solutions
for k=1:n % for each digit
% find the entries in the solutions vector x corresponding to digit k
% that have a value of 1 (i.e., the digit should be written in that box)
subx=find(x((k-1)*n^2+1:k*n^2));
for j=1:n % loop through
row=mod(subx(j),n);
if row==0
row=n;
end
S(row,j)=k;
end
end
% Sudoku Matrix S
S
Compare this to the solution we generated by hand earlier, and see that MATLAB succeeded in finding the same solution!

Next up is to try this with your own puzzles. The code has been copied below in one section for your convenience, with the sample 9x9 puzzle shown at the start encoded in the given matrix. Check that MATLAB can solve that as well, and try your own!
Further directions
Interested in exploring some other interesting questions related to this post? Here are some further directions to get you started:
- What happens if we don't add any givens to the linear program, i.e. we start with an empty Sudoku board? We should end up with a solution - is it unique? How might we interpret this solution? (The solver may take a bit longer to find the solution, but it will find a solution.)
- How might you impose other constraints to transform the Sudoku puzzle into something possibly more difficult? Two options might be: (a) requiring that each diagonal of the Sudoku grid contains each of the digits 1-9 once and only once, and (b) requiring that the middle boxes of each subgrid form their own subgrid requiring each of the digits 1-9 once and only once.
- Pick another variant of Sudoku and implement those constraints, such as if the subgrids are shaped differently.
Just the code
%n=4; % for 4 by 4 sudoku problem
n=9; % for 9 by 9 sudoku problem
Aeq=zeros(4*n^2, n^3);
%% Fill in Aeq for the n^2 constraints requiring that each element
% of the matrix must contain an integer 1:n
for i=1:n
for j=1:n
for k=1:n
Aeq((i-1)*n+j,(i-1)*n+j + (k-1)*n^2)=1;
end
end
end
%% Fill in Aeq for the n^2 constraints requiring that each row
% can have only 1 of each integer 1:n
for k=1:n
for i=1:n
for j=1:n
Aeq(n^2+i+(k-1)*n,1+(i-1)+(j-1)*n+(k-1)*n^2)=1;
end
end
end
%% Fill in Aeq for the n^2 constraints requiring that each column
% can have only 1 of each integer 1:n
for i=1:n^2
Aeq(2*n^2+i,(i-1)*n+1:i*n)=ones(1,n);
end
%% Fill in Aeq for the n^2 constraints requiring that each submatrix
% can have only 1 of each integer 1:n
for m=1:sqrt(n)
for l=1:sqrt(n)
for j=1:n
for k=1:sqrt(n)
Aeq(3*n^2+(m-1)*sqrt(n)*n+(l-1)*n+j,(j-1)*n^2+(l-1)*sqrt(n)+...
(m-1)*sqrt(n)*n+(k-1)*n+1:...
(j-1)*n^2+(l-1)*sqrt(n)+(m-1)*sqrt(n)*n+(k-1)*n+sqrt(n))=1;
end
end
end
end
% If any values of the Sudoku matrix are given, add these as
% constraints
% Enter each given value in matrix as triplet (row, col, integer)
% Example for 9-by-9 sudoku
Givens=[1 1 4;
1 2 9;
1 6 5;
1 9 1;
2 2 5;
2 7 7;
2 8 2;
2 9 9;
3 3 2;
3 6 8;
3 8 4;
3 9 5;
4 1 2;
4 3 8;
4 5 4;
4 6 3;
5 2 7;
5 4 8;
5 6 6;
5 8 3;
6 4 5;
6 5 9;
6 7 1;
6 9 8;
7 1 7;
7 2 8;
7 4 6;
7 7 4;
8 1 3;
8 2 4;
8 3 9;
8 8 6;
9 1 5;
9 4 3;
9 8 1;
9 9 7];
% turn these given elements into their appropriate position in the x vector
% of decision variables.
g=size(Givens,1);
for i=1:g
Aeq(4*n^2+i,Givens(i,1)+(Givens(i,2)-1)*n+(Givens(i,3)-1)*n^2)=1;
end
% beq=rhs vector (3n^2 by 1) for equality contraints
beq=ones(4*n^2+g,1);
%% run matlab's "intlinprog" command
numVariables = size(Aeq,2);
intcon = 1:numVariables;
lb = zeros(1,numVariables);
ub = ones(1,numVariables);
[x,fval,exitflag,output]=intlinprog(zeros(n^3,1),intcon,[],[],Aeq,beq,lb,ub);
exitflag;
output;
%% turn matlab's outputed solution vector x into sudoku terms
S=zeros(n,n);
for k=1:n
subx=find(x((k-1)*n^2+1:k*n^2));
for j=1:n
row=mod(subx(j),n);
if row==0
row=n;
end
S(row,j)=k;
end
end
% Sudoku Matrix S
S







评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。