今回はテクニカルコンサルティング部の本郷がお送りします。

---

はじめに

はじめまして。テクニカルコンサルティング部の本郷です。普段は物理モデリングを中心としたコンサルティング業務を担当しています。趣味は音楽、特にギター演奏です。といってもバンド演奏ではなく、フュージョン系・ロック系のコピーを DTM しています。ベースは弾かないので DTM する場合は音源を使いますが、最近は PCM 録音系以外に物理モデリング系のベース音源をよく使っています。と、無理やり物理モデリングの話題につなげてみました。

 さて、Simscape を使っていると「アクロス変数」や「スルー変数」という、普段あまり耳にしない用語に出会います。トレーニングやヘルプページで一応説明はあるものの、なぜこのような用語が Simscape で使われるのか不思議に思ったことはないでしょうか。

今回は、これらの用語について少し掘り下げてみたいと思います。

 

Simscape とは

まずは Simscape という製品について簡単におさらいしましょう。

一言で言えば、Simscape は物理モデリングのためのツールです。Simulink の上で動きます。電気・メカニカル・流体・熱など、異なる物理ドメイン(以下、マルチドメイン)を含む対象を直感的にモデリングできる製品です。

 

Simscape と Simulink での物理モデリングの違い

物理モデリングは、実は Simulink 単体でも可能です。では、Simulink と Simscape ではどんな違いがあるのでしょうか？

MathWorks の公式ドキュメントに、両者の比較例があります。これは力学系ではもっとも基本的な題材の一つ、マス・バネ・ダンパ系の例（Simulink と Simscape でのマス-バネ-ダンパー）です。

この例を参考に、違いを整理してみましょう。

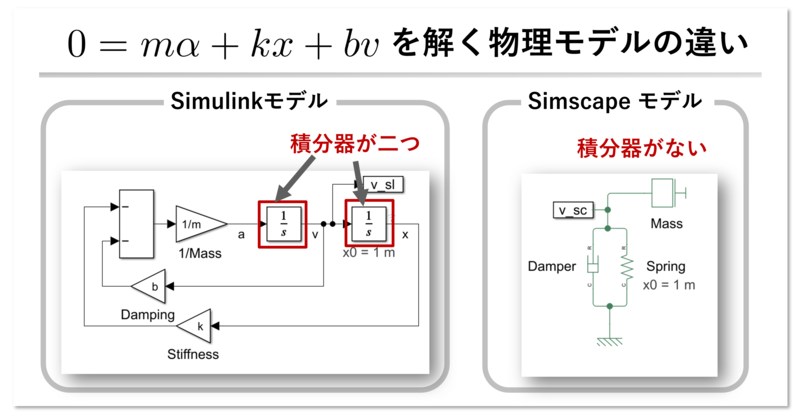
Simulink による物理モデル

Simulink モデルを見ると積分器が二つあることに気付きます。なぜ積分器が必要なのでしょうか？

このモデルは 0 = m a + k x + b v という方程式を解いています。ここで m は質量、k はバネ定数、b は減衰係数、a は加速度、v は速度、x は位置です。v や  x はそれぞれ a や v を積分して求める必要があります。つまり Simulink ではユーザー自身が積分器を配置し、方程式を意識しながらモデルを組み立てる必要があります。

 

Simscape による物理モデル

一方、Simscape のモデルは実際の構成イメージに近い配置でブロックが接続されています。積分器のブロックは見当たりませんね。これは、Simscape の各ブロックが自分自身の方程式を内部に持っているためです。シミューレーションを実行時には、Simscape が全ブロックをつなぐ連立方程式※を内部で自動的に生成し、計算を始めます。つまり、ユーザーは積分や方程式を意識せず、直感的にモデリングできるのが Simscape の特徴です。

(※ 正確には微分代数方程式なのですが、あまり馴染がないかも知れません。微分代数方程式は微分方程式と代数方程式のセットのことです。複数の方程式のセットというイメージを持ちやすいように、以下では連立方程式としておきます。ただし微分方程式と代数方程式のセットのことを指しています。)

 

Simscape と Simulink の違いまとめ

• Simulink: ユーザーが物理系の方程式や積分を意識しながらモデリングする必要があります。
• Simscape: ブロックごとに方程式が定義されており、連立方程式(微分方程式+代数方程式)は自動的に生成されます。ユーザーは構造を配置するだけで OK です。

 

連立方程式はどうやって自動生成される？

Simscape は内部で自動的に連立方程式を生成することを上で書きました。では、どうやって自動的に連立方程式を生成しているのでしょう。

ここで登場するのがアクロス変数とスルー変数の概念なのです。

Simscape が内部で連立方程式を自動生成する際に、次の「保存則」を適用して各ノード・ループで方程式を立てます:

• あるノードでのスルー変数の総和がゼロ
• あるループでのアクロス変数の総和がゼロ (あるいはノード間でアクロス変数が等しい)

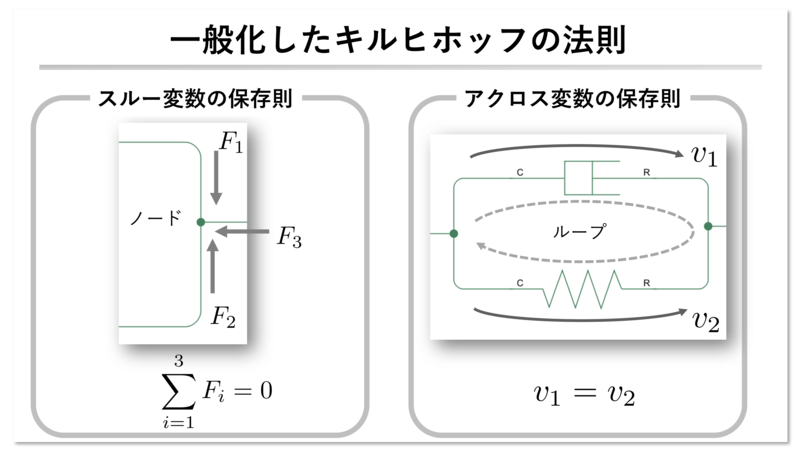
電気回路に馴染みがある人なら、これがキルヒホッフの法則そのものであることに気付くでしょう。

Simscape ではキルヒホッフの法則を電気以外の物理系にも拡張して※、各ノード・ループで方程式を生成し、モデル全体で連立方程式を構成します。

(※ある物理ドメインの挙動をそれ以外のドメインに拡張して物理を理解することをアナロジー(類推)と言うことがあります。末尾の参考情報をご参照下さい。)

各ブロックは内部で方程式を持っていますが、接続されたブロックの情報は持っていません。他のブロックとの接続の情報はノード、あるいはループの形成で表現されています。ノード・ループに保存則を課すことで、接続されているブロックどうしを数式で結びつけています。このようにSimscapeは一般化したキルヒホッフの法則を利用して複数のブロックの方程式を連立方程式にしています。

 

アクロス変数・スルー変数とは？

 

具体例

Simscape でのアクロス変数とスルー変数の例を示します:

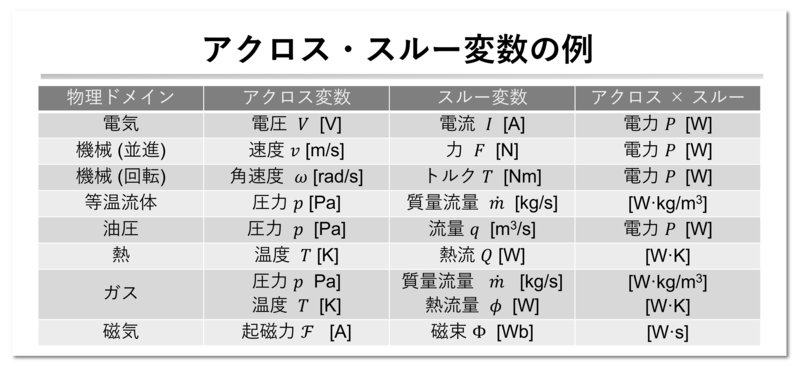
モデリングするうえでは、アクロス変数とスルー変数は各ループで総和がゼロになる(ノード間で等しい)/各ノードでの総和がゼロになる物理量、と覚えておくと良いでしょう。(上の表では、参考までにアクロス変数とスルー変数の積も計算しています。これについては後に述べます。)

 

よくある測定手法による説明

アクロス変数とスルー変数の説明としてよくあるのが、次のような測定手法による分類です:

• 「電圧のようにある要素の両端で測定する、あるいはある基準からの差を測定するものがアクロス変数」
• 「電流のように間に計測器を挿入して測定するものがスルー変数」

この分類はイメージしやすいですね。

トルクメーターと電流計の使い方は近いように思えます。しかし、力の測定(フォースゲージなど)が電流計と同じか…など突き詰めると、このような測定手法による分類は少し怪しい部分もありそうに思います。

 

アクロス変数×スルー変数=電力？

アクロス変数とスルー変数を掛け合わせると電力(ワット)になるドメインも多いです。ただし、全てのドメインで成立するわけではないので、参考程度に考えるのが良さそうです。一定の法則はあるようなので、掘り下げると楽しめるかもしれません

 

アクロス変数・スルー変数のメリット

 

連立方程式を自動的に構築できる

アクロス変数・スルー変数の考え方の利点は、上述のように、連立方程式を自動的に構築することに向いている点です。これは、拡張されたキルヒホッフの法則を各ノード・ループに適用することで可能になります。

異なるドメインでも統一的に方程式を構築できる

もう一つ重要なことは、異なるドメイン(電気・力学・流体など)でも、統一的に方程式を構築できる点です。

各ブロック内の方程式を生成し、各ノード・各ループでの保存則を課すというプロセスは異なるドメインでも共通となるからです。こうして、アクロス変数・スルー変数の考え方を利用すると、異なる物理ドメインでも自動的に連立方程式を構築するエンジンを作りやすくなります。これがマルチドメインの物理シミュレーターでアクロス変数・スルー変数の考え方が採用されている背景です。

 

難しさ・注意点

アクロス変数・スルー変数の考え方は万能ではなく難しい点もあります。最も躓(つまず)くのは、特に力学系ではあまり直感的でないことだと思います。もしかすると、個人差があるのでしょうか…。

個人的には、特に速度がアクロス変数、つまり電圧のアナロジー(類推)になることは直感的に理解しづらいと感じます。また、質量は電気回路とのアナロジーをイメージしづらいですね。アナロジーは必ずしも一対一対応があるわけではありません。理解の補助として考えておくのが良いでしょう。

 

まとめ

まとめると、アクロス変数・スルー変数は Simscape が内部で連立方程式を自動的に生成するための基本概念です。各要素(バネやダンパなど)の方程式に加えて、アクロス変数とスルー変数の保存則を適用すると、連立方程式が構成できます。各ドメインでアクロス変数とスルー変数を適切に設定すれば、異なるドメインでも連立方程式を統一的に構成できるのです。

言い換えると、これはドメインの異なる物理系を統一的に記述する「見方」の一つということです。

一方で、ドメインによってはアクロス変数・スルー変数の考え方は直感的でない場合もあります。Simscape での「道具立て」として割り切るのもアリと思います。

 

おわりに

Simscape で利用しているアクロス変数・スルー変数について私なりの解説を試みました。

MathWorks ではヘルプドキュメントに多くのモデリング例があるので、そちらを参照しながら実際に手を動かして Simscape に親しんでもらえると嬉しく思います。

 

(参考情報) アクロス変数・スルー変数の考え方の源流

アクロス変数・スルー変数の考え方は Simscape や MathWorks 独自のものではありません。Simscape 以外では、Modelica や 20-sim といった物理シミューレーションツールもこの考え方を利用しています。

アクロス変数・スルー変数の考え方は、1933 年に Firestone が最初に力学系と電気系のアナロジーを論じたものが最初です。もともとは、電気系の挙動を考察するために馴染のある力学系の物理学との類推を活用しようとしたのが出発だったようです。当時はオシロスコープなどの可視化の道具がなかったため、力学系より遥かに高速に振る舞う電気系を理解するために力学系を利用したかった背景があったとのこと。

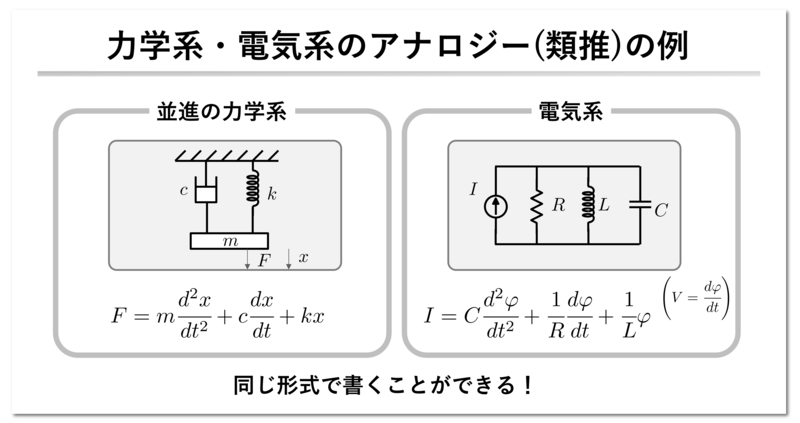
異なる物理ドメイン間のアナロジーについては文献1をご参照下さい。アクロス変数・スルー変数のアナロジー以外にも Maxwell の力=電圧のアナロジーなどの説明があります。

 

[1] R. H Bishop, Mechatronics: An Introduction