Spatial transformations: Handling noninvertible cases
I've written previously about how imtransform uses inverse mapping to compute the input-space location corresponding to each output pixel. I've also written about how imtransform uses the forward mapping to determine the location of the output image in output space.
But what about noninvertible mappings? For example, the function cp2tform can produce several types of spatial transformations that aren't invertible. It can infer a polynomial transformation from a set of control points:
pairs1 = [1 1; 5 21; 17 40; 28 1; 32 20; 45 40; 72 1; 77 20; 90 40]; pairs2 = [1 1; 1 21; 1 40; 20 1; 20 20; 20 40; 40 1; 40 20; 40 40]; t_poly = cp2tform(pairs1, pairs2, 'polynomial',2); I = checkerboard(10, 2); J = imtransform(I,t_poly); subplot(1,2,1) imshow(I), title('checkerboard') subplot(1,2,2) imshow(J), title('polynomial transformation')

But the polynomial transformation isn't invertible. Since imtransform uses inverse mapping and so must have at least the inverse transformation, cp2tform produces a tform structure where the polynomial transformation is used in the inverse direction, and the structure contains nothing for the forward direction.
t_poly
t_poly =
ndims_in: 2
ndims_out: 2
forward_fcn: []
inverse_fcn: @inv_polynomial
tdata: [6x2 double]
If there's no forward transformation available, then how does findbounds work? That is, how does it find the bounding rectangle of the image in output space?
It does it by using a search. Specifically, for an input-space location u, it uses fminsearch to find the output-space location x that minimizes:
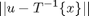
It's possible fminsearch might fail to converge, in which case findbounds issues a warning message and "guesses" that the output image's bounding rectangle is the same as the input image's bounding rectangle.
If you're interested in the details, look at the find_bounds_using_search subfunction inside findbounds.m.








评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。