The sci.image.processing newsgroup had a discussion this week on separable filters, which reminded me that separability has been on my blog topic ideas list for a while now.

Contents

What is a separable filter?

A two-dimensional filter kernel is separable if it can be expressed as the outer product of two vectors. For example, let's look at a Sobel kernel.

s = [-1 0 1; -2 0 2; -1 0 1]

s =

    -1     0     1
    -2     0     2
    -1     0     1

This kernel can be written as a matrix product of a column and a row vector.

v = [1; 2; 1]

v =

     1
     2
     1

h = [-1 0 1]

h =

    -1     0     1

v * h

ans =

    -1     0     1
    -2     0     2
    -1     0     1

Associativity of convolution

As it turns out, the matrix product of a column vector and a row vector is equivalent to the two-dimensional convolution of the two vectors.

conv2(v, h)

ans =

    -1     0     1
    -2     0     2
    -1     0     1

This matters because convolution is associative. That is,

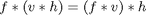
(I've used the asterix here to mean convolution.) So if a filter s is separable:

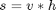
then you can filter with s by filtering first with v, and then filtering the result with h.

Computational advantage of separable convolution

Why would you want to filter this way? Because you can do it faster. Filtering an M-by-N image with a P-by-Q filter kernel requires roughly MNPQ multiplies and adds (assuming we aren't using an implementation based on the FFT). If the kernel is separable, you can filter in two steps. The first step requires about MNP multiplies and adds. The second requires about MNQ multiplies and adds, for a total of MN(P + Q).

The computational advantage of separable convolution versus nonseparable convolution is therefore:

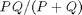
For a 9-by-9 filter kernel, that's a theoretical speed-up of 4.5.

That's enough for now. Next time, I'll write about how to determine whether a filter kernel is separable, and what MATLAB and toolbox functions test automatically for separability.

Get the MATLAB code

Published with MATLAB® 7.3