The sci.image.processing newsgroup had a discussion this week on separable filters, which reminded me that separability has been on my blog topic ideas list for a while now.
Contents
What is a separable filter?
A two-dimensional filter kernel is separable if it can be expressed as the outer product of two vectors. For example, let's look at a Sobel kernel.
s = [-1 0 1; -2 0 2; -1 0 1]
s =
-1 0 1
-2 0 2
-1 0 1
This kernel can be written as a matrix product of a column and a row vector.
v = [1; 2; 1]
v =
1
2
1
h = [-1 0 1]
h =
-1 0 1
v * h
ans =
-1 0 1
-2 0 2
-1 0 1
Associativity of convolution
As it turns out, the matrix product of a column vector and a row vector is equivalent to the two-dimensional convolution of the two vectors.
conv2(v, h)
ans =
-1 0 1
-2 0 2
-1 0 1
This matters because convolution is associative. That is,
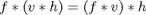
(I've used the asterix here to mean convolution.) So if a filter s is separable:
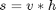
then you can filter with s by filtering first with v, and then filtering the result with h.
Computational advantage of separable convolution
Why would you want to filter this way? Because you can do it faster. Filtering an M-by-N image with a P-by-Q filter kernel requires roughly MNPQ multiplies and adds (assuming we aren't using an implementation based on the FFT). If the kernel is separable, you can filter in two steps. The first step requires about MNP multiplies and adds. The second requires about MNQ multiplies and adds, for a total of MN(P + Q).
The computational advantage of separable convolution versus nonseparable convolution is therefore:
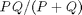
For a 9-by-9 filter kernel, that's a theoretical speed-up of 4.5.
That's enough for now. Next time, I'll write about how to determine whether a filter kernel is separable, and what MATLAB and toolbox functions test automatically for separability.
Get
the MATLAB code
Published with MATLAB® 7.3
Hi Steve,
I would like to know more about 2D seperable filters, have u got any reference sites to recommend?
In addition, if i am using remez () in matlab to design 1D FIR filter and then usetrans() to transform it to a 2D Filter, is this a seperable or non-seperable filter? In general, how do I create a 2D separable filter?
Thanks alot
Foo
Foo – I have reference books, not reference sites. :-) For example, Multidimensional Digital Signal Processing, by Dudgeon and Mersereau. The book Digital Image Processing Using MATLAB talks about separability, but not in any more detail than I’ve given here. You should also look at my separability – part 2 post. It discusses how to detect separability.
I’m not sure which function you are referring to for creating a 2-D filter. It looks like there’s a typo in your comment. Can you clarify?
A filter is separable if it has rank 1, so you can use the MATLAB function rank> to see whether a given filter is separable.
You can create a separable filter by forming the outer product of two 1-D filters.
Hi Steve:
I wanna construct a blur matrix by using ‘conv2′ command,however, my matrix is sparse matrix that ‘conv2′ doesn’t support, So, is there other similar functions I can use?
Woo – I’m not aware of MATLAB functions for performing convolution on sparse matrices. You could possibly implement something yourself, based the notion of convolution as a sum of weighted and shifted versions of the convolution filter.
Dear sir how to perform Polygonal approximation of an image using matlab?
Shan—Can you be more specific? What are your inputs; what specific problem do you want to solve; how do you want your outputs expressed?
Steve,
You talked about advantage of being separable without using fft. How about the comparison of separable and nonseparble 2D convolution with the aid of fft? Thanks.
Dan—Filter separability makes no practical difference when using the FFT to perform convolution. The 2-D FFT is separable anyway, regardless of the properties of the filter. In fact, MATLAB performs all multidimensional FFTs by exploiting the separability of the transform.
Hi Steve
When you convolve two matrices f and g using conv2 the dimension of f*g is more than f and g. so if i wanna deconvolve what do i need to do? g=iff2(fft2(f*g)./fft2(f)) does not agree in dimension. If I do zero padding then it does not give the right result. Thanks
Kaushal—Even if you get the padding right, you’ll have problems if fft2(f) has zero values or very small values. You might want to take a look at Stan Reeves’ deblurring series in this blog.
sir
how can I convolve an image with blurring filter [0.25 .5 0.25]
Reji—Use imfilter in the Image Processing Toolbox, or use conv2 or filter2 in MATLAB.
sir
i used imfilter to convolve the image in each dimension.i’m trying to implement an algorithm for my research work.in the algorithm I want to blur and scale down an image.in the algorithm they used the filter[0.25 0.5 0.25].sir what type filter is this?
I = imread(‘peppers.png’)
figure;imshow(I);
h=[0.25 0.5 0.25];
blur1_m=imfilter(I, h,’conv’);
figure;imshow(blur1_m);
I used this program to convolve the image with [0.25 0.5 0.25] in each direction.the result i’m getting had no much difference with the original one
reji
Reji—If you filter with [0.25 0.5 0.25], each pixel is replaced 0.5 times itself plus 0.25 times its left neighbor plus 0.25 times its right neighbor. The filter will have a small smoothing effect.
Sir, I am trying to convolve an image with a gaussian derivative kernel for edge detection. Is there any fast way to do this? Thanks
Ray—If you search for “fast Gaussian filtering algorithms” you should see several papers describing techniques.
Can you help me to perform 2d convolution of a large image (10000×10000) with conv2 matlab function.
Hi Steve,
I am just entering the image processing realm and have what is probably a very basic question.
Let G_MxM be a separable filter given by
Gx_MxM = d_Mx1 * s_1xM,
where “*” denotes matrix multiplication.
The result of filtering [1] an input matrix X at row n and column m by
this Gx matrix is then
Yx_M(n,m) = X_M(n,m) * Gx
= X_M(n,m) * d * s
= (X_M(n,m) * d) * s,
where X_M(n,m) and Yx_M(n,x) are the MxM matrices at n, m.
Further expanding this gives
Yx(n,m) = s(m) * \sum_{k = 0}{M – 1} X(n, m + k) d(k),
where X(n,m) and Yx(n,m) are the elements of the matrices X and Yx at row
n and column m, respectively.
Now note that the product of X_M and d is a 1D convolution of the filter
d along the nth row of X_M, and the value s(m) simply scales that
convolution.
Thus if d is the simple 1D difference filter [1 0 -1] (as it is for a
Sobel filter), then this operation produces the derivative of X_M along
the nth row of X_M, or what I would call the gradient in the x
direction.
Fine. Great.
But then, if Gy = Gx’, as it is here for a Sobel filter,
http://en.wikipedia.org/wiki/Sobel_operator
then the gradient in the y direction is
Yy_M(n,m) = X_M(n,m) * Gy
and therefore
Yy(n,m) = d(m) * \sum_{k = 0}{M – 1} X(n, m+k) s(k).
By the same mathematics as above, we see that the product
of X_M and s is a 1D convolution of the filter s along
the nth row of X_M.
But this is NOT the gradient of X in the y direction, since such a
gradient would have to be performed on the COLUMNS of X.
So from this reasoning, it seems that to determine the x-gradient
of X we should compute
X * Gx
but to determine the y-gradient of X we should compute
Gy * X.
Is this correct? If so, then isn’t is also true that to perform these
gradients correctly one must have a side-specific image filter
operation? Specifically, my question is, if this is true, how can the
Matlab/Octave image processing library’s imfilter(X,Gx) and
imfilter(X,Gy) compute both gradients correctly, since it presumably
multiplies on only one “side” and thus one would be incorrect?
–Randy
[1] We ignore various details such as edge effects and the sign-reversal
that standard convolution requires here to simplify the notation and
presentation.
Steve, ignore that previous post – i was getting confused between the multiplication operator and the convolution operator.
Hey Steve, thanks for the insight into separable kernels. I would like to know how what you have written in the initial posts applies to 3D.
For instance I have a 3D mask and intend to convolve with a guassian. I know that the gaussian is separable, how do I go about separating the kernel for convolution in 3D ?
regards
GT
GT—Just filter three times in succession. Use a one-dimensional Gaussian filter oriented along the 1st dimension, then along the 2nd dimension, then along the 3rd.
Hi Steve,
Concerning the built-in n-D convolution methods:
MATLAB (v2008b) keeps failing due to out-of-memory errors when convolving large 3D arrays (e.g. (256)^3) with a ~16^3 (general, non-separable) kernel.
I’ve tried imfilter, convn or convnfft from the filexchange, same result …
Would it make sense to add an functionality that transparently breaks down the task into filtering smaller sub-arrays and stitches together the results, depending on the free contiguous memory blocks, to prevent memory errors? Or can you think of another solution ?
Thanks
Vasek
Vasek—I believe convn does not use extra memory besides that required for the input and output arrays. So if you are running out of memory with convn, a block-based approach will not help you. You might want to look at the “Avoiding Out of Memory Errors” support page for more information and tips.
Hi Steve,
You describe how to determine if a filter is separable in the time domain. What if I have an filter in the frequency domain only, and want to recognize if it is separable, and possibly write the h1 and h2 components of the filter in the time domain, whithout using ifft2?
Hi Steve, I was wondering whether or not this content of this article relates at all to a Separability filter – read it in a paper and I have not been able to get a clear definition.
Thanks!
Jonathan—If you mean “separable filter,” then yes, that is the same thing as separable convolution.