Relationship between continuous-time and discrete-time Fourier transforms
Previously in my Fourier transforms series I've talked about the continuous-time Fourier transform and the discrete-time Fourier transform. Today it's time to start talking about the relationship between these two.
Let's start with the idea of sampling a continuous-time signal, as shown in this graph:

Mathematically, the relationship between the discrete-time signal and the continuous-time signal is given by:

(When I write equations involving both continuous-time and discrete-time quantities, I will sometimes use a subscript "c" to distinguish them.)
The sampling frequency is  (in Hz) or
(in Hz) or  (in radians per second).
(in radians per second).
The discrete-time Fourier transform of  is related to the continuous-time Fourier transform of
is related to the continuous-time Fourier transform of  as follows:
as follows:

But what does that mean? There are two key pieces to this equation. The first is a scaling relationship between  and
and  :
:  . This means that the sampling frequency in the continuous-time Fourier transform,
. This means that the sampling frequency in the continuous-time Fourier transform,  , becomes the frequency
, becomes the frequency  in the discrete-time Fourier transform. The discrete-time frequency
in the discrete-time Fourier transform. The discrete-time frequency  corresponds to half the sampling frequency, or
corresponds to half the sampling frequency, or  .
.
The second key piece of the equation is that there are an infinite number of copies of  spaced by
spaced by  .
.
Let's look at a graphical example. Suppose  looks like this:
looks like this:

Note that  equals zero for all frequencies
equals zero for all frequencies  . This is what we mean when we say a continuous-time signal is band-limited. The frequency
. This is what we mean when we say a continuous-time signal is band-limited. The frequency  is called the bandwidth of the signal.
is called the bandwidth of the signal.
The discrete-time Fourier transform of  looks like this:
looks like this:

where  . As I mentioned before, normally only one period of
. As I mentioned before, normally only one period of  is shown:
is shown:

For this example, then,  between
between  and
and  looks just like a scaled version of
looks just like a scaled version of  .
.
Next time we'll consider what happens when  doesn't look like
doesn't look like  . In other words, we're about to tackle aliasing.
. In other words, we're about to tackle aliasing.



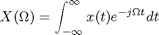





댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.