Changes to SUM and DIM
Does this line of code make you raise your eyebrows in puzzlement?
c = sum(A,[1 2])
If so, you are likely an experienced MATLAB user who does not make a habit of carefully studying the release notes, line by line, every six months. So, let me tell you about this change to sum and other related functions.
I think of sum as a vector-wise function. Its basic definition is expressed in terms of its operation on a vector: sum(v), where v is a vector, returns a scalar that is the sum of the elements of v.
v = [1 2 3 4 5 6]; sum(v)
ans =
6 times 7 divided 2, silly.
For sum and many, many other functions, MATLAB has a forgiving definition of the term "vector." It can refer to a single column (Px1) or a single row (1xP). The expression sum(v) doesn't care.
w = v' sum(w)
w =
1
2
3
4
5
6
ans =
you can't fool me, the answer is still 21.
How about sum on a matrix? We just love magic squares around here, especially when we're talking about sums.
A = magic(3)
A =
8 1 6
3 5 7
4 9 2
What does sum(A) do? Remember what I said earlier - I think of sum as a vector-wise function, meaning that fundamentally it operates on vectors. If you pass it a matrix, it will treat that matrix as a stack of vectors. Specifically, it will treat the matrix as a stack of column vectors, computing the sum of each of them.
sum(A)
ans =
15 15 15
For the last two decades (and just a bit more), the sum function has accepted an optional argument that we call DIM. This argument lets you change the way sum treats a matrix (or a multidimensional array) as a stack of vectors. For example, the call sum(A,2) tells sum to treat A as a stack of row vectors and compute the sum of each one, result in a column vector containing row sums.
sum(A,2)
ans =
15
15
15
Of course, a magic square has the same row sums as column sums, which is why a magic square was probably a bad choice for this example. However, my employment contract requires that I use magic(3) at every opportunity.
Now, suppose I have an RGB image, F, which is MxNx3, and I want to compute the sum of each of the three component images, F(:,:,1), F(:,:,2), and F(:,:,3)? For most of MATLAB history, this is what we would tell you to do: Compute the column sums and then compute the row sums of the result. (Or, you could do it the other way 'round and get the same answer.)
F = imread('peppers.png');
c = sum(sum(F,1),2)
c(:,:,1) =
23746472
c(:,:,2) =
13054194
c(:,:,3) =
11331211
OK, suppose I want to compute the sum of all the elements of F? The historical answer: convert F to a single column vector using the expression F(:) and then call sum.
sum(F(:))
ans =
48131877
But those coding patterns are SO R2018a. With the R2018b release, DIM can be a vector, and it call also be the string "all" (or 'all'). Computing the sum of the each of the three component images can now be:
sum(F,[1 2])
ans(:,:,1) =
23746472
ans(:,:,2) =
13054194
ans(:,:,3) =
11331211
And computing the sum of all of the elements of the three-dimensional array can be:
sum(F,[1 2 3])
ans =
48131877
or
sum(F,"all")
ans =
48131877
After you have summed everything in sight that seems to need summing, you can check out these other MATLAB vector-wise functions that also have this new DIM behavior: all, any, bounds, max, min, mean, median, mode, prod, std, and var.
Let me leave you with a little bit of programming advice related to these functions. If you are certain that the input argument you are passing to one of these functions is a vector (because you constructed or computed it yourself), then you can safely use the single-input syntax, like sum(v). Otherwise, I recommend that you always provide the optional DIM argument to avoid certain ambiguities associated with MATLAB's forgiving definition of "vector."




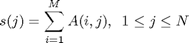


Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.