Today's blog post comes from planning one topic, but then taking a sharp left turn and doing something else completely. I was thinking about writing something related to meshgrid, and so I was looking at some old blog posts in which meshgrid was used. For example, meshgrid was used in this 30-Dec-2010 post about the a* and b* component in the Lab color space. In reading over that old post, however, I realized that I made a rather egregious conceptual error in it. I plotted colors over the domain $ -100 \leq a^* \leq 100 $, $ -100 \leq b^* \leq 100 $, using $ L^* = 90 $, without realizing or explaining that most of those $ (L^*,a^*,b^*) $ combinations are far out of the sRGB gamut. In other words, they are not really displayable (even on a wide-gamut monitor). Also, the functions I used back then have since been superseded by new functions that are not only easier to use, but are also more helpful at looking at in-gamut vs. out-of-gamut questions.
I decided, therefore, to update and improve that old post.
Showing $ (a^*,b^*) $ colors for a fixed $ L^* $
As I did last time, I'll start with $ L^*=90 $, which is at the bright end of the scale. For that choice of $ L^* $, let's see what the colors in the $ (a^*,b^*) $ plane look like, taking into account colors that might be out of gamut.
In the old post, I used makecform and applycform to convert Lab values to sRGB values. This time, I'll use lab2rgb.
When using lab2rgb, out-of-gamut values are indicated by output values that are greater than 1 or less than 0.
out_gamut_mask = any((rgb > 1) | (rgb < 0),3);
Let's replace the out-of-gamut colors with gray and display the result. Set the y-direction of the image display to 'normal' so that positive $ b^* $ is at the top, which is the usual convention for these kinds of plots. Also, display the axes ticks and labels.
rgb(repmat(out_gamut_mask,1,1,3)) = 0.6;
imshow(rgb,'XData',b,'YData',a)
xlabel('$a^*$','Interpreter','latex')
ylabel('$b^*$','Interpreter','latex')
title('$L^*=90$','Interpreter','latex')
As you can see, with $ L^*=90 $, only a relatively small portion of the $ (a^*,b^*) $ plane is in gamut.
Yellow is the brightest color
Let's repeat that process with an even brighter $ L^* $ value, almost all the way to white.
out_gamut_mask = any((rgb > 1) | (rgb < 0),3);
rgb(repmat(out_gamut_mask,1,1,3)) = 0.6;
imshow(rgb,'XData',b,'YData',a)
xlabel('$a^*$','Interpreter','latex')
ylabel('$b^*$','Interpreter','latex')
title('$L^*=96$','Interpreter','latex')
The plot above demonstrates that yellow is the only color that can be displayed almost as bright as white.
Blue is the darkest color
Now let's try something dark.
out_gamut_mask = any((rgb > 1) | (rgb < 0),3);
rgb(repmat(out_gamut_mask,1,1,3)) = 0.6;
imshow(rgb,'XData',b,'YData',a)
xlabel('$a^*$','Interpreter','latex')
ylabel('$b^*$','Interpreter','latex')
title('$L^*=25$','Interpreter','latex')
Although you can make out some relatively unsaturated green and red regions above, blue is the only fully saturated color.
What is the in-gamut $ (a^*,b^*) $ region for every $ L^* $?
Now, I want to make multidimensional cubes of $ L^* $, $ a^* $, and $ b^* $ values over their entire ranges and calculate the in-gamut colors all at once.
Find $ L^* $, $ a^* $, $ b^* $ values filling a three-dimensional region. Convert the triples to sRGB.
[LL,bb,aa] = ndgrid(L,b,a);
rgb = lab2rgb([LL(:) aa(:) bb(:)]);
Reshape so that the color component is in the 4th dimension. Make a three-dimensional out-of-gamut mask. Replace out-of-gamut values with gray.
rgb = reshape(rgb,[size(LL) 3]);
mask = any((rgb > 1) | (rgb < 0),4);
rgb(repmat(mask,1,1,3)) = 0.6;
Display the set of colors for $ L^*=50 $ (corresponding to the index 51 in the first dimension). After indexing with 51 in the first dimension, use squeeze to eliminate that dimension before displaying as an image.
rgb_50 = squeeze(rgb(51,:,:,:));
imshow(rgb_50,'XData',b,'YData',a)
xlabel('$a^*$','Interpreter','latex')
ylabel('$b^*$','Interpreter','latex')
title('$L^*=50$','Interpreter','latex')
Here's an animation, creating using imwrite, showing the in-gamut colors for the values of $ L^* $ ranging from 0 to 100.
What is the in-gamut $ L^* $ range everywhere in the $ (a^*,b^*) $ plane?
These experiments caused me to wonder how to visualize the range of colors more broadly, while keeping the visualization in the $ (a^*,b^*) $ plane. Here's a relevant question: given particular $ a^* $ and $ b^* $ values, what is the lowest $ L^* $ value that is in gamut? What is the highest value? Further, can we tell if no $ L^* $ values are in gamut for a particular $ a^* $ and $ b^* $?
I worked this out based on the multidimensional arrays computed above.
Find the minimum in-gamut values in the LL array along the first dimension, taking advantage of the fact that the min function ignores NaN values by default. Use the squeeze function to eliminate the first dimension, which has a size of 1 following the min operation.
LL_min = squeeze(min(LL_min,[],1));
Following a similar procedure, find the maximum in-gamut values in the LL array along the first dimension.
LL_max = squeeze(max(LL_max,[],1));
Here are the darkest and brightest in-gamut $ L^* $ values on the $ (a^*,b^*) $ plane, displayed with a grayscale colormap, along with the associated colors.
imshow(LL_min,[],'XData',a,'YData',b)
title('Minimum in-gamut $L^*$','Interpreter','latex')
xlabel('$a^*$','Interpreter','latex')
ylabel('$b^*$','Interpreter','latex')
imshow(LL_max,[],'XData',a,'YData',b)
title('Maximum in-gamut $L^*$','Interpreter','latex')
xlabel('$a^*$','Interpreter','latex')
ylabel('$b^*$','Interpreter','latex')
rgb_min = lab2rgb(cat(3,LL_min,aa,bb));
imshow(rgb_min,'XData',a,'YData',b)
xlabel('$a^*$','Interpreter','latex')
ylabel('$b^*$','Interpreter','latex')
rgb_max = lab2rgb(cat(3,LL_max,aa,bb));
imshow(rgb_max,'XData',a,'YData',b)
xlabel('$a^*$','Interpreter','latex')
ylabel('$b^*$','Interpreter','latex')
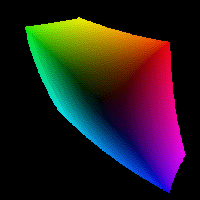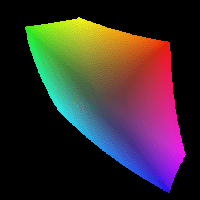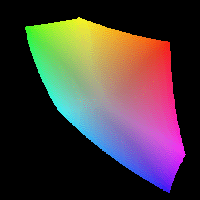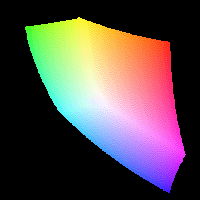
Finally, I want to make an animation showing how the colors in the above plot change as they go from the darkest available color to the lightest, starting with another four-dimensional cube of RGB images:
rgb_scan = zeros([size(bb2) 3 (N+1)]);
LL_diff = LL_max - LL_min;
L_k = LL_min + (LL_diff * (k/N));
rgb_scan(:,:,:,k+1) = lab2rgb(cat(3,L_k,aa2,bb2));
Here's the resulting animation, also created using imwrite. (Note that quality of the animation suffers because of the GIF limitation of no more than 256 distinct colors in each frame.)















评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。