Integrating to find the volume underneath a set of nonuniformly spaced data
This video covers the use of GRIDDATA, anonymous functions, and QUAD2D to integrate the volume under a set of randomly spaced data points. First an interpolation scheme must be put in place, then a numeric quadrature function is invoked.
This video shows the creation of a good synthetic data set with a known volume to test the rest of the algorithm. A good test data set like this really give confidence in the building of your algorithm.
% I have a dataset "A" (n by 3) of ordered triplets [x,y,z].
%I want to calculate the volume between surface defined by "A" and
%the xy plane. "A" has only positive values but is not uniformly
%spaced and not gridded. "A" cannot be described by a simple
%function. Any help?
n = 10;
randOffset = 0.1;
h = 1;
x = rand(n);
x(1:4)=[0 1 0 1]';
y = rand(n);
y(1:4)=[0 0 1 1]';
z = h + randOffset*rand(n) - randOffset/2; %make average height
plot3(x,y,z,'.')
axis equal
zlim([0 h + randOffset])
interpZ = @(xi,yi) griddata(x,y,z,xi,yi) %set up interpolation
interpZ(0.5,0.5) %test interpolation
vol = quad2d(interpZ,0,1,0,1) %volume should be close to 1
Note: there is an update to this post here:
https://blogs.mathworks.com/videos/2009/09/18/revisited-integrating-to-find-the-volume-underneath-a-set-of-non-uniformly-spaced-data/ 




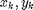



评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。