Autonomous Navigation with Brian Douglas, Part 2: Heuristic vs Optimal Approach for Full Autonomy
What is autonomous navigation? we learnt that in the last post of this blog series. In this one, Brian will talk about different types of autonomy and the approaches we can take to achieve full autonomy. If you are looking to go one level deeper in understanding the basics of autonomous navigation, this post is for you.
Hi, I’m Brian Douglas and welcome to the Autonomous Navigation blog. If you haven’t read the first blog from this series, please take a look here.
Autonomy can have various levels. Within on-road motor vehicle automated driving systems, or simply put self-driving cars, there are 6 levels of driving automation as defined by SAE International. However, for this blog, let’s describe the levels of autonomy more generally as a spectrum rather than as discrete levels that are specific to self-driving cars. We can think of autonomy as spanning from autonomy assistance at the low end of the spectrum up to a fully autonomous vehicle at the high end.
For autonomy assistance, a vehicle is mostly operated by a human, perhaps even from a remote location, but there are algorithms on board that will monitor for unsafe conditions and autonomously override the operator to place the vehicle in a safe state. In this way, the human operator is doing most of the navigating, but there are some autonomous actions that take over in certain situations.
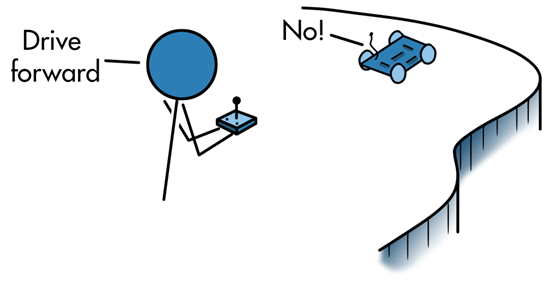
On the other end of the autonomy spectrum, we have a fully autonomous vehicle. This is a vehicle that is capable of navigating through an environment with no human intervention at all. It can sense the environment and reach some destination through its own decision-making processes.
However, even fully autonomous vehicles aren’t created equal. We can approach full autonomy in two different ways; a heuristic approach and an optimal approach.
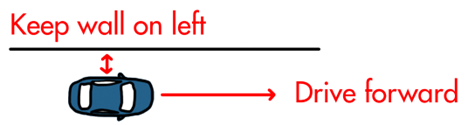
With a heuristic approach, autonomy is accomplished by giving the vehicle a set of practical rules or behaviors that it follows. An example of a heuristic approach to autonomy is a maze solving robot that has been given two rules to follow: drive forward and keep a wall to its left.
To accomplish this, the robot could have two sensors that measure distance: one facing forward, and one facing to the left. Using these sensors and some logic the vehicle could follow a wall at a fixed distance, turn left when the wall turns left, make a U-turn at the end of a wall, and turn right at a corner. In this way, the vehicle will proceed to wander up and down the hallways until it happens to reach the goal.
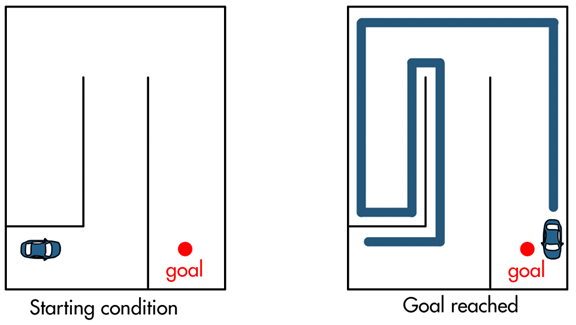
Heuristic approaches like this can navigate through a maze and without a human having to control it (full autonomy), however, heuristic approaches don’t guarantee an optimal result. The path the vehicle took wasn’t the shortest or the most distance-optimal. Other issues with a heuristic approach is that the given rules may not be sufficient for all conditions within an environment. For example, it’s easy to set up a situation where our maze solving robot gets stuck in a loop and never reaches the goal.
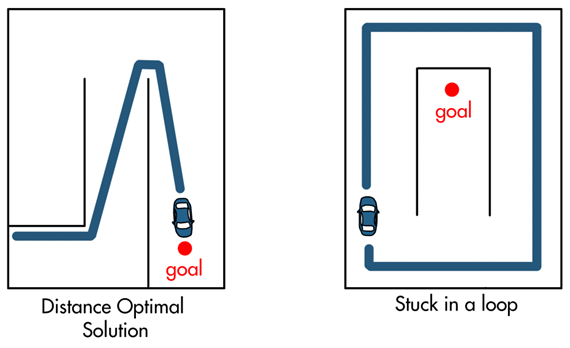
Those are some of the downsides of a heuristic approach, however, a benefit is that you don’t need complete information about the environment to accomplish full autonomy. The vehicle didn’t have to create or maintain a map of the maze (or even know that it’s in a maze!) to reach the goal.
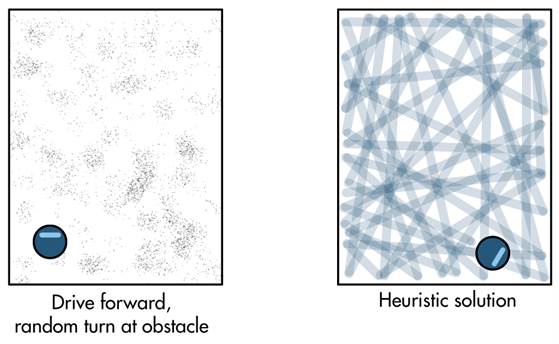
Other types of heuristic-based autonomy include things like the simplest of robotic vacuums. When the vacuum approaches an obstacle like a wall, a rule tells it to rotate to a new random angle and then keep driving straight.
As time increases, the chance that the entire floor is covered approaches 100 percent. Therefore, in the end, the goal of having a clean floor is met, even if the vehicle doesn’t take the optimal path to achieve it.
Let’s contrast the heuristic approach with the optimal approach to autonomous navigation.
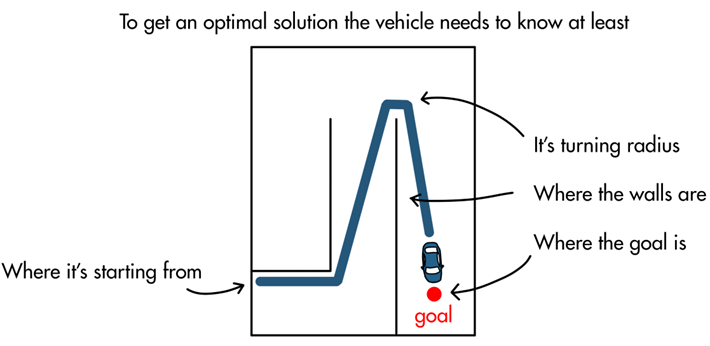
First off, optimal doesn’t necessarily mean the best. All it means is that we’re creating some objective that we want to accomplish and then algorithmically trying to find a solution that maximizes or minimizes the value of that objective. For example, we may want the vehicle to travel along the shortest path to the goal. In that case, we would set up a function that penalizes distance traveled. And then, through some chosen optimization technique, we would search through or sample the entire set of possible paths that the vehicle could take and select the path that produces the lowest cost, or in our case, the lowest distance.
Objective: Minimize distance traveled to the goal given the turning constraints of the vehicle
These types of problems typically require more knowledge of the environment and the limitations and constraints of the vehicle because you need to know that information to explore and bound the problem space. For example, the vehicle can’t find the shortest distance to the goal if it doesn’t have a good understanding of the entire environment. The vehicle also can’t produce a path that it can actually follow if it doesn’t understand its turning radius or how fast it can accelerate. Therefore, solving for the optimal solution requires that the vehicle have a lot more information.
In many cases, optimal-based strategies produce a much better result than their heuristic-based counterparts and therefore, it justifies the burden of having to set it up. Possibly the most common example of this at present is autonomous driving where a vehicle has to navigate to a destination through dynamic and chaotic streets. Relying on simple behaviors like driving forward and keeping the curb to your left is probably not the best approach to reach your destination safely and quickly. It makes more sense to give the vehicle the ability to sense and model the dynamic environment, even if that model is imperfect, and then use it to determine an optimal navigation solution.
Now that we have an idea of the different types of autonomy, in the next post we’re going to continue our introduction to autonomous navigation systems by looking at the capabilities of autonomous systems and discussing how sometimes the best solution is a combination of both heuristic and optimal approaches.
To learn more about autonomy and different types of autonomous systems, check out this video on “How to Build an Autonomous Anything“. Stay tuned for the next post from Brian!
- Category:
- Autonomous Navigation with Brian Douglas
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.