Floating Point Arithmetic Before IEEE 754
In a comment following my post about half-precision arithmetic, "Raj C" asked how the parameters for IEEE Standard 754 floating point arithmetic were chosen. I replied that I didn't know but would try to find out. I called emeritus U. C. Berkeley Professor W. (Velvel) Kahan, who was the principle architect of 754. Here is what I learned.
Contents
The Zoo
First, some background. George Forsythe, Mike Malcolm and I wrote a textbook published in 1977 that began with a chapter on floating point computation. The chapter includes the following table of the floating point parameters for various computers. The only copy of the original book that I have nearby has some handwritten corrections, so I scanned the table in the Greek translation.
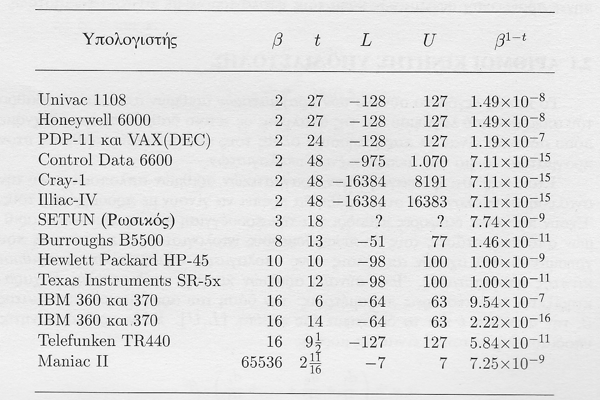
This was before personal computers and IEEE 754. It was a real zoo. There were binary and decimal and even a Russian ternary machine. There were a variety of word lengths. Among the binary machines, there were base 2, base 8 and base 16 normalizations.
IEEE 754
Around 1976 Intel began development of the 8086 microprocessor, which would become the CPU chip in the first IBM PCs. John Palmer (who had been a student of mine in New Mexico) was in charge of the design of the 8087 floating point coprocessor. He recommended that Kahan become a consultant. Palmer and Kahan convinced Intel to take the unprecedented step of making their design public so that it could be an industry wide standard. That Intel specification became the basis for IEEE 754.
I wrote a two-part series in this blog about 754 floating point and denormals.
Kahan's Parameters
Kahan told me that he chose the design parameters for the 8087 and consequently for the 754 standard. He said he looked at industry practice at the time because he wanted existing software to move to the new processor with a minimum of difficulty. The 32- and 64- bit word lengths were dictated by the x86 design. There were two architectures that came close to his vision, the IBM 360/370 and the DEC PDP-11/VAX.
So, the zoo was reduced to these two. Here are their floating point radix beta and exponent and fraction lengths.
single double
beta exp frac exp fracIBM 360 16 7 24 11 52
DEC VAX F 2 8 23 DEC VAX D 2 8 55 DEC VAX G 2 11 52
IEEE 754 2 8 23 11 52
Nobody was happy with the base-16 normalization on the IBM. Argonne's Jim Cody called it "wobbling precision". The DEC VAX had two double precision formats. The D format had the same narrow exponent range as single precision. That was unfortunate. As I remember it, DEC's G format with three more bits in the exponent was introduced later, possibly influenced by the ongoing discussions in the IEEE committee.
The VAX F format for single and G format for double have the same bit lengths as the Palmer/Kahan proposal, but the exponent bias is different, so the resulting realmax and realmin differ by a factor of four. DEC lobbied for some flexibility in that part of the standard, but eventually they had to settle for not quite conforming.
Retrospect
Looking back after 40 years, the IEEE 754 was a remarkable achievement. Today, everybody gratefully accepts it. The zoo has been eliminated. Only the recent introduction of a second format of half precision has us thinking about these questions again.
Thanks, Raj, for asking.
- Category:
- Numerical Analysis,
- People,
- Precision






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.