A few days ago, a bug report from our office in Cambridge caught my attention. Computing the singular values and singular vectors of a particular matrix would sometimes cause MATLAB to crash.

Contents

Two Computers

I use two different computers regularly. The machine in my home office is a Lenovo ThinkPad® model T14, loaded with two external monitors, several external disc drives, a sound bar and a dedicated internet connection. My traveling machine is a Lenovo ThinkPad X1 Nano with no external hardware.

The report of a crash in the SVD became even more interesting when I found that it happens on my office computer, but not on the portable. A quick check revealed that the CPUs on the two machines come from different manufacturers. The office computer uses an AMD® Ryzen Pro 5 while the traveling machine uses an Intel® Core i7.

Math Libraries

The crash occurs several software layers deep in CGESVD, the LAPACK driver for single precision complex SVD. Various chip manufacturers provide math libraries that have been optimized for their CPUs. However, by default, MATLAB uses the reportedly faster Intel Math Kernel Library, MKL. It is possible to switch to other math libraries.

We have experts at MathWorks who know far more about the details of these libraries than I do. They will soon sort this all out. In the meantime, here is what I have learned about the offending matrix.

G3366394

We refer to the matrix in the crash report by its case number in our bug tracking system. The matrix is of modest size but is otherwise unusual for several reasons. It is rectangular with fewer rows than columns, it is in single precision, and it is complex.

  clear
  load g3366394 X
  whos

  Name        Size              Bytes  Class     Attributes
  X         219x384            672768  single    complex

The following code calling SVD with three outputs will crash MATLAB on my T14, but not on my X1.

  trysvd = false
  if trysvd
      [U,S,V] = svd(X);
      R = U*S*V' - X;
      relres = norm(R)/norm(X)
  end

  trysvd =
    logical
      0

Rank

Computing the singular values without the vectors can be done on either machine. The following code uses double precision and then plots the singular values on a logarithmic scale with a line at single precision roundoff level.

  S = svd(X);
  semilogy(S,'.-')
  ep = eps('single');
  line([0 230],[ep ep])
  axis([0 230 1e-15 10])
  legend({'singular values','eps(''single'')'})

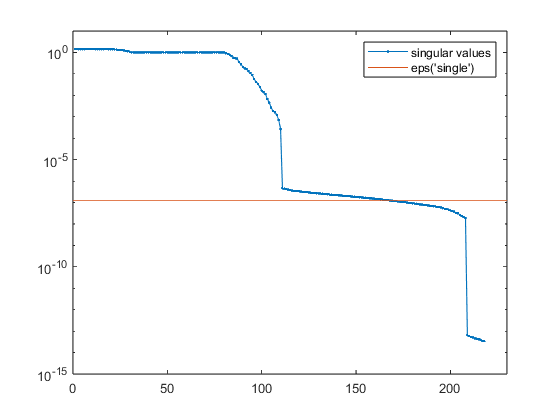
We see that the matrix is far from full rank. About half of its singular values are negligible. This is confirmed by

   xrank = rank(X)

   xrank =
      110

Zero rows

The cause of the low rank is easy to find. This surf plot reveals that almost half of the rows are flat zero.

Let's remove the zero rows.

  c = sum(abs(X),2)==0;
  nnzc = nnz(c)
  X(c>0,:) = [];

  nnzc =
     109

The remaining matrix is full rank and it is safe to compute its singular vectors.

  [U,S,V] = svd(X);
  R = U*S*V' - X;
  resnorm = norm(R)

  resnorm =
     2.8191e-06

Fuzz

Removing the zero rows was the first work-around that I tried. There are many others. You can replace the zeros with any nonzero "fuzz".

  fuzz = 1.e-20;
  [U,S,V] = svd(X + fuzz*randn(size(X)));

  resnorm = norm(U*S*V'-X)

  resnorm =
     2.8222e-06

Flip

You can reorder the matrix so that the zero rows are not at the beginning.

  [U,S,V] = svd(flipud(X));
  U = flipud(U);

  resnorm = norm(U*S*V'-X)

  resnorm =
     2.3809e-06

Now what?

How to avoid the crash is not the most important question. What causes the crash with the original matrix? We will find out and get it fixed.

Get the MATLAB code

Published with MATLAB® R2024a