An Algorithmic Spelling Bee

저자 Ned Gulley, April 6, 2023

47 회 조회 (최근 30일) | 0 좋아요 | 9 댓글

Earlier this year I wrote about solving word ladders with MATLAB. There was a lot of interest in that post, so I thought I'd share my investigations regarding another word-based app. In this script, I'm trying to create a puzzle modeled on the NY Times Spelling Bee game. Here is the premise: you are given seven letters, and your job is to find all possible words you can make with those seven letters. You can use letters more than once, but they must be four or more letters long, and they must all include the special center letter. Every Spelling Bee puzzle has at least one "pangram", which is a word that uses all seven letters.

As an example, suppose you were given this puzzle.

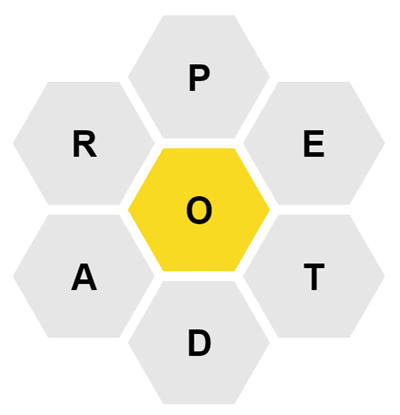
From this puzzle you could create PORE, ADORE, ADOPT, as well as the pangram OPERATED. But you couldn't create POD (too short) or PAPER (doesn't include the center letter "O").

Here I'm not so much interested in solving the puzzle. I want to write a script that can create a Spelling Bee puzzle.

Build the Dictionary

We need some ground truth for all the legal words. Here's Google's 10,000 word English dictionary. It's small, but good enough for our purposes here.

url = 'https://raw.githubusercontent.com/first20hours/google-10000-english/master/google-10000-english.txt';

wordList = webread(url);

Split the word list into strings.

words = split(string(wordList));

words = lower(words);

The Spelling Bee puzzle avoids the letter S so that it never has to deal with plurals. Let's use logical indexing to keep only the words that don't contain an S.

keep = ~words.contains("s");

words = words(keep);

Of these, keep only the words that are four letters or longer.

keep = words.strlength >= 4;

words = words(keep);

I like how these string commands are easy to read and understand! Just like for us humans, code that communicates clearly keeps its job the longest. We don't want to employ fussy, high-maintenance code.

How many words do we end up with?

fprintf("The adjusted dictionary now contains %d words\n",length(words))

The adjusted dictionary now contains 4955 words

We've thrown out about half the words in our dictionary.

We'll be converting from ASCII representation to alphabet number a few times, so let's invest in a little anonymous helper function. It'll make the code below a little easier to read.

% An anonymous function to translate ASCII values to A=1, B=2, ... Z=26.

ascii2letter = @(chars) abs(lower(chars))-96;

Try it out

ascii2letter('ABCXYZ')

ans = 1×6
1 2 3 24 25 26

Looks good!

Build a 26-column sparse matrix to represent unique letter usage for each word. Each word in the dictionary gets one row. Every letter that appears in the word gets a 1.

dictionaryLength = numel(words);

a = sparse(dictionaryLength,26);

for i = 1:dictionaryLength

 uniqueLetters = unique(words(i).char);

 a(i,ascii2letter(uniqueLetters)) = 1;

end

nnz(a)/numel(a)

ans = 0.2218

At 22% full, this matrix isn't terribly sparse as sparse matrices go. But it's a fun excuse to play with SPARSE, so let's carry on. Here's a SPY plot of the matrix.

spy(a)

set(gca, ...

 XTick=1:26, ...

 XTickLabel=num2cell('A':'Z'), ...

 XTickLabelRotation=0, ...

 XAxisLocation="top", ...

 PlotBoxAspectRatio=[1 1 1])

To make much out of this, we need to zoom in. Let's see how the word LABEL is encoded.

ix = 1002;

% In case you're wondering, I like to use "ix" as short for "index"

words(ix)

ans = "label"

full(a(ix,:))

ans = 1×26
1 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0

spy(a(1001:1010,:))

xline([1 2 5 12])

yline(2,Color="red")

set(gca, ...

 XTick=1:26, ...

 XTickLabel=num2cell('A':'Z'), ...

 XTickLabelRotation=0, ...

 XAxisLocation="top", ...

 YTick=1:10, ...

 YTickLabels=words(1001:1010))

Note that even though the L appears twice in the word, it only has a one in the matrix.

Just for fun, let's do a histogram of the letters. This can be a useful sanity check that we're on the right track.

allLetters = ascii2letter(char(join(words,'')));

histogram(allLetters)

set(gca, ...

 XTick=1:26, ...

 XTickLabel=num2cell('A':'Z'), ...

 XTickLabelRotation=0)

As expected, E is the most commonly appearing letter. Q is the least, but for the fact that we completely wiped out S.

How many words are composed of exactly seven distinct letters? That is, how many are potential pangrams for a game?

% Summing letter-use across the rows

% Use FIND to build an index to all the words that use exactly seven letters

ix7LetterWords = find(sum(a,2)==7);

length(ix7LetterWords)

ans = 790

Let's look at a few of these seven-letter words.

num7LetterWords = numel(ix7LetterWords);

ix = ix7LetterWords(1:10);

disp(words(ix(1:10)))

"product"

"privacy"

"company"

"project"

"american"

"network"

"following"

"including"

"location"

"profile"

Pick a good one as the "seed" pangram for our game.

ix = ix(9);

disp(words(ix))

location

How many words can be spelled from those same 7 letters? Find all the words that use nothing but the letters in the seed word

lettersInSeedWord = a(ix,:);

% Find all the words that have none of the letters from the seed word.

% We're making sure that all contributions of letters other than

% the seed letters sum to zero.

ixWordsFromSeedWord = find(sum(a(:,~lettersInSeedWord),2) == 0);

fprintf('%d words use only the seven letters appearing in the seed word.\n',numel(ixWordsFromSeedWord))

73 words use only the seven letters appearing in the seed word.

Which letters appear most frequently?

bar(sum(a(ixWordsFromSeedWord,:)))

set(gca, ...

 XTick=1:26, ...

 XTickLabel=num2cell('A':'Z'), ...

 XTickLabelRotation=0)

We need to designate one letter as the "center letter" that must appear in every word. Let's pick the letter that appears least frequently.

vals = full(sum(a(ixWordsFromSeedWord,:)));

vals(vals==0) = inf;

[~,ixlet] = min(vals);

centerLetter = char(ixlet+96);

Remove all the words that don't have this letter

ixRequired = find(a(:,ixlet));

ix2a = intersect(ixWordsFromSeedWord,ixRequired);

This is the original seed word:

fprintf("%s\n", words(ix))

location

Here are the seven unique letters:

sevenLetters = unique(char(words(ix)));

fprintf("%s\n", sevenLetters);

acilnot

The required center letter is:

fprintf("%s\n", upper(centerLetter));

C

Here are the pangrams

ix3 = find(sum(a(ix2a,:),2)==7);

for i = 1:numel(ix3)

 fprintf("%s\n",words(ix2a(ix3(i))));

end

location

coalition

allocation

Here is the complete list of words

for i = 1:numel(ix2a)

 fprintf("%s\n",words(ix2a(i)));

end

contact

local

location

call

action

cool

clinical

canon

icon

contain

atlantic

cotton

lincoln

clinton

cincinnati

clinic

coalition

coat

allocation

ncaa

coal

oclc

coin

citation

colin

ciao

cant

canal

colonial

clan

italic

incl

colon

cannon

Some of those are little odd, but we have our dictionary to thank for that.

sixLetters = setdiff(sevenLetters,centerLetter);

sixLetters = sixLetters(randperm(6));

Now for the graphics! Make the plot

% The perimeter hex cells are centered from pi/6 to 11*pi/6 radians

t = 2*pi*(0:5)/6 + 2*pi/12;

r = 1.08*sqrt(3);

x = r*cos(t);

y = r*sin(t);

cla

hexplot(0,0,upper(centerLetter),"#F7DA21")

hold on

for i = 1:numel(x)

 hexplot(x(i),y(i),upper(sixLetters(i)),"#E6E6E6")

end

hold off

axis equal

axis off

And there you have it! It's easy to see how valuable a good algorithmically generated game can be. Once you've worked out the logic, you just need to run it once every day and your puzzle is ready to go. Compare this with the labor that goes into a crossword puzzle. Although who knows? Maybe crossword puzzles will be yet another of those things that AI proves to be adept at.