Guest Blog by: Peetak Mitra, Dr. Majid Haghshenas and Prof. David P. Schmidt
The following is an accepted paper at the Neural Information Processing Systems (NeurIPS) Machine Learning for Engineering Design, Simulation Workshop 2020. This work is a part of the ICEnet Consortium, an industry-funded effort in building data-driven tools relevant to modeling Internal Combustion Engines. More details can be found at icenetcfd.com
In recent years, there has been a surge of interest in using machine learning for modeling physics applications. Prof. Schmidt’s research group at UMass Amherst has been working towards applying these methods for turbulence closure, coarse-graining, combustion or building cheap-to-investigate emulators for complex physical process. In this blog, we will introduce the current challenges in applying mainstream machine learning algorithms to domains specific applications and will showcase how we dealt with this challenge in our scientific application of interest that is the closure modeling relevant to fluid turbulence.
Current Challenges
The ML algorithms and the best practices in designing the network and choosing hyperparameters therein, have been developed for applications such as computer vision, natural language processing among others. The loss manifold of these datasets is by nature vastly different than the one observed in the scientific datasets [see Figure 1 for an example, loss generated using a function of two variables, obtained by translating and scaling Gaussian distributions, a common distribution in science and engineering]. Therefore, often times these best practices from literature translate poorly to applications within scientific domain. Some major challenges in doing so include that the data used to develop machine learning algorithms differ from scientific data in fundamental ways; as the scientific data is often high-dimensional, multimodal, complex, structured and/or sparse [1]. The current pace of innovation in SciML is additionally driven by and limited to, the empirical exploration/experimentation with these canonical ML/DL techniques. In order to fully leverage the complicated nature of the data as well as develop optimized ML models, automatic machine learning (AutoML) methods for automating network design and choosing the best performing hyperparameters is critically required. In this work, we explore the effectiveness of Bayesian based AutoML methods for complex physics emulators in an effort to build robust neural network models.
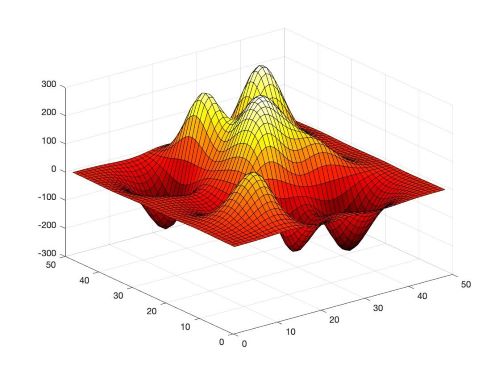
Fig 1. A non-convex loss manifold, showing multiple local regions of optimum making the neural network training process difficult
Our application and proposed solution: Our scientific application of interest is fluid turbulence, which is a non-linear, non-local, multi-scale phenomenon [see Figure 2 for the typical range of scales in simulation] and is an essential component of modeling engineering-relevant flows such as in Internal Combustion Engine [see Figure 2 for the range of scales typical in an ICE simulation]. While solving the full Navier Stokes using Direct Numerical Simulation (DNS) results in the most accurate representation of the complicated phenomenon, DNS is often computationally intractable. Engineering level solutions based on Reynolds Averaged Navier-Stokes (RANS) and Large Eddy Simulations (LES) alleviate this issue by resolving the larger integral length scales and modelling the smaller unresolved scales by introducing a linear operator to the Navier-Stokes equation to reduce the simulation complexity. These models however suffer from the difficulty of turbulence closure. In this study, we demonstrate the capability of DNNs to learn LES closure, as a function of filtered variables.
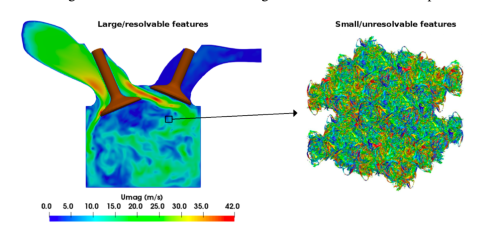
Fig 2. This figure shows the multi-scale nature of turbulence in a typical Internal Combustion Engine simulation. Figure adopted from Dias Ribeiro et al. [1]
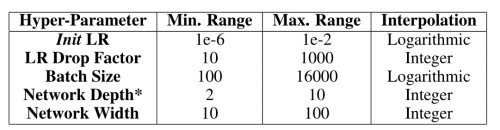
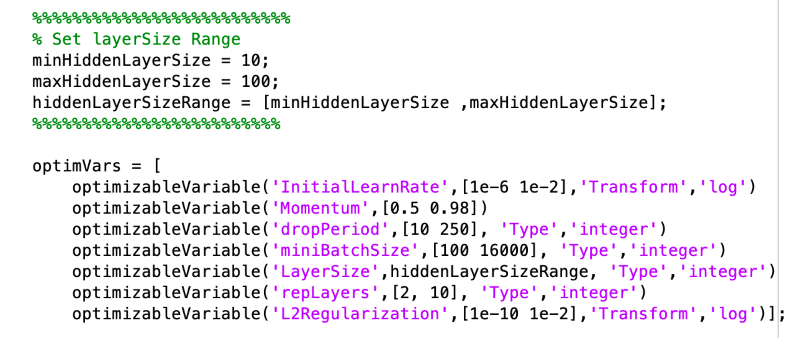
Network design and optimization: In order to optimize the network architecture and identify best hyperparameter settings for this task, we use a Bayesian Optimization based autoML framework, in which the learning algorithm’s generalization performance is modeled as a sample from a Gaussian Process (GP) [For reference, Figure 3 lays out the entire workflow]. Expected Improvement is used as the acquisition function, to identify the next settings of parameters to investigate. Key learning parameters, including learning rate, drop factor, batch size, and network architecture, which have a leading order effect on the convergence, are optimized. The table below shows the ranges of parameters and the interpolation scheme used to investigate the next parameters. The code implementation in MATLAB is shown following that. The Bayesian Optimization process is run sequentially on each set of parameters. Within each optimization run, the network is trained and performance against validation data are evaluated, at the end of training.
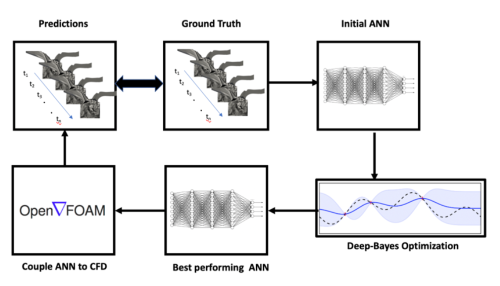
Fig 3. An end-to-end workflow used in the study. An autoML method based on Bayesian Optimization is used to identify best performing network settings and architecture, which is then integrated into OpenFOAM and comparisons made to the ground truth data, in an
a-priori and
a-posteriori setting.
In order to optimize the network architecture, a block of network in Fully Connected Layer, and leakyRelu activation layer are used. The depth of the network and the width (number of neurons in each layer) are further optimized using the Bayesian Optimization, during each run.

Results
We find that the ADAM Glorot and ADAM He combinations perform the best in terms of absolute errors, although the ADAM Glorot configuration has the highest number of parameters. The RMPSProp on average, performs better than SGDM optimizer. This can be explained as RMSProp is an adaptive learning rate method and is capable in navigating regions of local optima and whereas that SGDM performs poorly navigating ravines and makes hesitant progress towards local optima. The a-priori performance of the best performing model is shown in Figure 4.
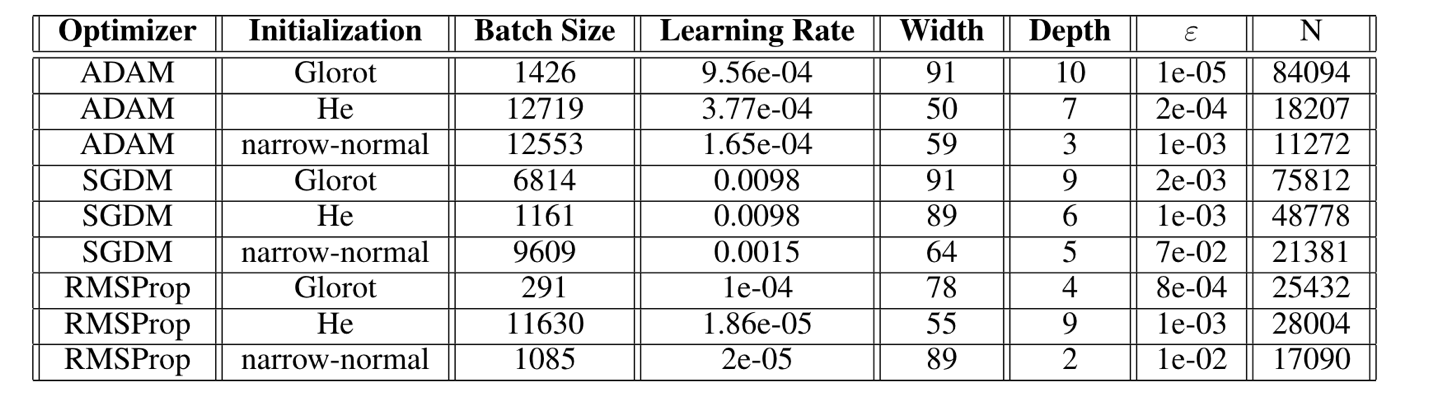
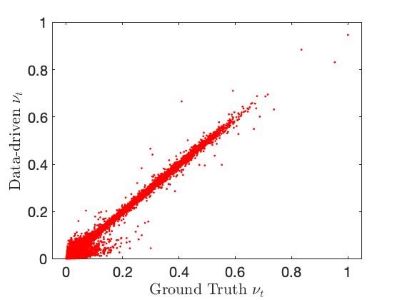
Fig 4. The
a-priori testing shows the performance of the data-driven predictions, to the ground truth eddy viscosity predictions.
To better understand the learning process, we compute cosine similarity between weights checkpointed during training process after every epoch. This investigation [seen in Figure 5] reveals the self-similarity in the learning process each set of weight initialization-optimizers setting. However, when compared between different sets of optimizers, the differences in the learning process are clear.
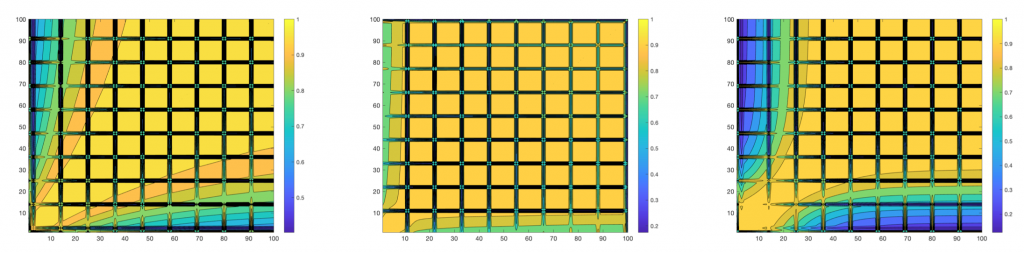 Fig 5. Evolution of the learning process can be visualized using the cosine similarity during the network training checkpointed at every epoch.
Fig 5. Evolution of the learning process can be visualized using the cosine similarity during the network training checkpointed at every epoch.
Since neural network weights are often multi-dimensional, to visualize the learning process, a dimensionality reduction technique such as t-SNE is useful in exploring the function-space. The effect of initialization is clearly evident from Figure 6, the Glorot and He initializations have overlapping function-space behavior which is expected due to the similarities in their mathematical formulation. Narrow-normal on the other hand is limited to only exploring a limited function-space. The optimizers show a wider variety in their function space exploration, and as seen previously the SGDM explores a limited set of the loss manifold whereas the other two optimizers explore a much wider range.
Fig 6. Low-dimensional representation of the function-space similarity for the weight initialization and optimizers reveal important takeaways.
In summary, an AutoML in the training loop, provides a pathway to not only build robust neural networks suitable for applications to scientific datasets, but can be used to better understand the network training evolution process.
To learn more about our work please follow the pre-print here, and watch the NeurIPS 2020 ML4Eng workshop spotlight talk here.
References
[1]: Dias Ribeiro, Mateus, Alex Mendonça Bimbato, Maurício Araújo Zanardi, José Antônio Perrella Balestieri, and David P. Schmidt. "Large-eddy simulation of the flow in a direct injection spark ignition engine using an open-source framework." International Journal of Engine Research (2020): 1468087420903622








 Fig 5. Evolution of the learning process can be visualized using the cosine similarity during the network training checkpointed at every epoch.
Fig 5. Evolution of the learning process can be visualized using the cosine similarity during the network training checkpointed at every epoch.

 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.