Performance Review Criteria 3: Scales to the task
To scale or not to scale. That is the question. When talking about algorithmic complexity, the answer to said question is usually an important one. No matter what the constant factors are that affect your algorithm's speed, poor scaling performance severely limits the scope of the problems you can solve. How do you measure your code's runtime complexity? If you don't have a good method for this (or even if you do!) then once again the performance testing framework is on your side. I was amazed when I learned of this one weird trick to measure the complexity of my algorithms.
The (not so) secret here is that now that performance tests are tests, performance tests can be parameterized tests! Leveraging this feature we can simply send in the size of the problem as the parameter. Let's see how this is done.
Contents
The Code
To start, we need some code to scale. Let's look at a simple function that will allow us to simulate some work:
function doSomeWork(n) % Simple function that mimics some constant-time work to be done. pause(n); end
With this little "working" function, we now can play with some algorithms of different time complexity. First, let's look at something that is $\mathcal{O}(1)$, or constant time:
function constantTimeFunction(~) doSomeWork(.2); end
Easy enough. Note how the constantTimeFunction takes in a parameter but simply ignores it. This parameter is intended to be the size of the problem, and this function ignores it because constant time algorithms are the same regardless of size. How can we make something $\mathcal{O}(n)$, or linear? Put it in a for loop around the size of the problem:
function linearTimeFunction(n) for idx = 1:n doSomeWork(0.001); end end
Now don't worry about the example constants here. They really can be anything I've simply tweaked them to get something reasonable for this demonstration. OK, moving on let's create a $\mathcal{O}(n^2)$ quadratic time function by using two for-loops around the size:
function quadraticTimeFunction(n) for idx1 = 1:n for idx2 = 1:n doSomeWork(0.0001) end end end
How do we create something that is $\mathcal{O}(\log{}n)$? One way is to simply decrease the number of iterations so that as the problem size grows there is less work to do per unit of size. This can look like this:
function logTimeFunction(n) doSomeWork(0.001); while n > 1 n = n/2; doSomeWork(0.01) end end
Now, finally let's show something with $\mathcal{O}(2^{n})$, or exponential complexity. Recursion is a nice fallback whenever you want (!) an exponential algorithm.
function exponentialTimeFunction(n) doSomeWork(1e-4); for idx = 1:round(n) exponentialTimeFunction(idx-5); end end
Alright, now that we have all of our "code", let's see how we can evaluate how it scales. You can do this pretty easily by creating a performance test that uses a problemSize property as TestParameter. If this property contains the different parameter data in either a cell array or a structure if you'd like to give each point an intent revealing label. For this test lets just create a few points across the first couple decades. Once this parameter is defined, its trivially easy to pass it into the performance test methods and get your results:
classdef ScalingTest < matlab.perftest.TestCase properties(TestParameter) problemSize = num2cell(round(logspace(0,2,10))); end methods(Test) function testConstantTime(~, problemSize) constantTimeFunction(problemSize); end function testLogTime(~, problemSize) logTimeFunction(problemSize); end function testLinearTime(~, problemSize) linearTimeFunction(problemSize); end function testQuadraticTime(~, problemSize) quadraticTimeFunction(problemSize); end function testExponentialTime(testCase, problemSize) testCase.assumeLessThan(problemSize, 50); testCase.startMeasuring; exponentialTimeFunction(problemSize); testCase.stopMeasuring; end end end
Let's get our data and look at each algorithm individually. I can do this by calling runperf with the 'Name' option with some wildcards to narrow down on each method of interest, starting with the constant algorithm:
constantResult = runperf('ScalingTest', 'Name', '*testConstantTime*');
Running ScalingTest .......... .......... .......... .......... .......... .......... .......... .......... Done ScalingTest __________
Let's create a little helper function to get at the minimum value for each size. This will help us quickly pull out the data points. I am going to choose the minimum of each sample because it is Tuesday and Tuesday told me it really likes mins.
findMins = @(resultArray) arrayfun(@(result) min(result.Samples.MeasuredTime), resultArray); ax = axes; ylabel('Execution time (s)'); xlabel('Problem Size'); hold on; grid on; problemSize = [ScalingTest.problemSize{:}]; plot(ax, problemSize, findMins(constantResult), 'LineWidth', 2); leg = legend({'$\mathcal{O}(1)$'}, 'Interpreter', 'latex');

This looks all over the place until you realize the scale is off. Adjusting the y axis to start at zero shows its pretty flat.
ax.YLim(1) = 0;

Alright now we can start adding the more complex algorithms and see how they compare. Next logarithmic:
logResult = runperf('ScalingTest', 'Name', '*testLogTime*'); plot(ax, problemSize, findMins(logResult), 'LineWidth', 2); axis tight; leg = legend([leg.String '$\mathcal{O}(\log{} n)$'],'Interpreter','latex');
Running ScalingTest .......... .......... .......... .......... .......... .......... .......... .......... .... Done ScalingTest __________

Then linear:
linearResult = runperf('ScalingTest', 'Name', '*testLinearTime*'); plot(ax, problemSize, findMins(linearResult), 'LineWidth', 2); axis tight; leg = legend([leg.String '$\mathcal{O}(n)$'],'Interpreter','latex');
Running ScalingTest .......... .......... .......... .......... .......... .......... .......... .......... ........ Done ScalingTest __________
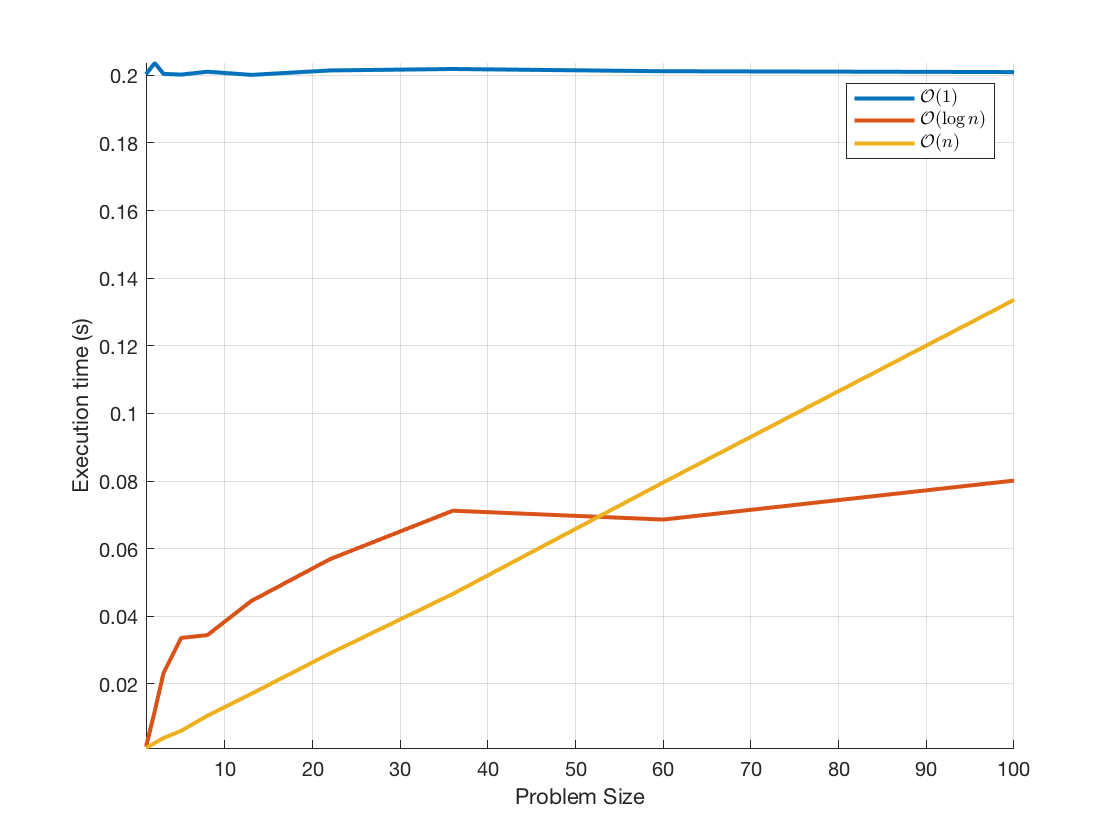
Then quadratic:
quadraticResult = runperf('ScalingTest', 'Name', '*testQuadraticTime*'); plot(ax, problemSize, findMins(quadraticResult), 'LineWidth', 2); axis tight; leg = legend([leg.String '$\mathcal{O}(n^2)$'],'Interpreter','latex');
Running ScalingTest .......... .......... .......... .......... .......... .......... .......... .......... .......... Done ScalingTest __________

...and finally exponential. Note that since the exponential blows up so quickly we needed to limit the problem size by using an assumption. Since we don't want to time the assumption, we are explicitly setting the measurement boundary to exclude the assumption call. For those sizes that fail the assumption, the result's Valid property will be false, so we can use that to trim the data for only the valid measurements we collected.
exponentialResult = runperf('ScalingTest', 'Name', '*testExponentialTime*'); valid = [exponentialResult.Valid]; validResult = exponentialResult(valid); validSize = problemSize(valid); plot(ax, validSize, findMins(validResult), 'LineWidth', 2); leg = legend([leg.String '$\mathcal{O}(2^n)$'],'Interpreter','latex');
Running ScalingTest
..........
..........
..........
..........
..........
..........
..........
..........
..
================================================================================
ScalingTest/testExponentialTime(problemSize=value9) was filtered.
================================================================================
.
================================================================================
ScalingTest/testExponentialTime(problemSize=value10) was filtered.
================================================================================
.
Done ScalingTest
__________
Failure Summary:
Name Failed Incomplete Reason(s)
===================================================================================================
ScalingTest/testExponentialTime(problemSize=value9) X Filtered by assumption.
---------------------------------------------------------------------------------------------------
ScalingTest/testExponentialTime(problemSize=value10) X Filtered by assumption.

It is now clear that trying to see this on a linear scale is getting ridiculous. Let's go log scale.
ax.YScale = 'log';

There we go! Here is the scale of all of our dummy algorithms. As you can see, the algorithmic complexity is very important. As the problem sizes scale, large constant factors quickly become irrelevant.
The Sum of all its parts
However, just for kicks lets do some MATLAB fun to find the constant factors. If you can't improve the algorithm's complexity, perhaps you might want to see where the constant factors are in order to see ways to improve the experience for achievable problem sizes. Well, in MATLAB this can be done using the ever beautiful matrix left divide. First lets put all of this code into one function and gather the scalability data
function complexFunction(n) constantTimeFunction(n); logTimeFunction(n); linearTimeFunction(n); quadraticTimeFunction(n); exponentialTimeFunction(n); end
Now let's write the test and gather the runtime data
classdef FullComplexityTest < matlab.perftest.TestCase properties(TestParameter) problemSize = {1, 2, 3, 5, 8, 13, 22}; end methods(Test) function testComplexFunction(~, problemSize) complexFunction(problemSize); end end end
additiveResult = runperf('FullComplexityTest'); problemSize = [FullComplexityTest.problemSize{:}]; executionTime = findMins(additiveResult); % Start with a fresh axes delete(ax) ax = axes; ylabel('Execution time (s)'); xlabel('Problem Size'); hold on; grid on; plot(ax, problemSize, executionTime, 'o');
Running FullComplexityTest .......... .......... .......... .......... .......... ...... Done FullComplexityTest __________

Does it fit?
Now let's fit the data! Note that $y= k_0 + k_1\log{}n + k_2n + k_3n^2 + k_42^n$
format long n = problemSize.'; y = executionTime.'; X = [ones(size(n)), log(n), n, n.^2, 2.^n]; k = X\y N = (0:0.1:22)'; Y = [ones(size(N)), log(N), N, N.^2, 2.^N]*k; plot(ax, N,Y,'-','LineWidth',2);
k = 0.203249252542941 0.024019014853585 -0.000703911764008 0.000243945808296 0.000000018436312

...and there we go. Lookin' good.
What do you think, do you see yourself analyzing how your MATLAB code scales using this technique?
- Category:
- Performance,
- Testing









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.