Quantum Computing for Optimizing Investment Portfolios
The following post is from Sofia Ma, Senior Engineer for Finance
Quantum computing is a cutting-edge field of study that harnesses the principles of quantum mechanics to perform complex computations exponentially faster than classical computers, holding immense promise for solving problems across various industries. The finance sector has been one of those that have shown early interest. With the release of the Quantum Computing support package in the latest version of MATLAB, we at MathWorks, would like to provide an overview of Quantum Computing for Portfolio Optimization in MATLAB.
The outline of this blog:
- Demystifying Quantum Computing: A brief journey into the fundamental concepts and evolution of quantum computing, setting the stage for understanding its immense potential.
- A Quantum Leap in Portfolio Optimization: Delving into a real-world example that demonstrates how quantum computing can revolutionize portfolio optimization, bringing unprecedented speed and efficiency.
- Deep Dive: Expanding Your Quantum Knowledge: A collection of curated resources for those intrigued by quantum computing and its application in financial portfolio optimization, encouraging further exploration and learning.
Demystifying Quantum Computing
Introduction
Quantum computing stands poised to revolutionize many sectors, not least of which is finance. In particular, it promises to transform the way we optimize investment portfolios, offering the ability to solve more complex problems faster and with superior quality results.
At the heart of this technological revolution is quantum computing’s potential to handle larger, more intricate computations at unprecedented speeds. Quantum computers utilize quantum bits, or “qubits,” which are the fundamental building blocks. Superposition and entanglement, inherent to qubits, enable the representation and manipulation of multiple states simultaneously, resulting in exponentially faster information processing and heightened computational power. This intrinsic parallelism allows quantum machines to process vast amounts of information exponentially faster than their classical counterparts.
In practical terms, it signifies that tasks that would take traditional computers years or even centuries to complete can potentially be executed in mere seconds on quantum machines, which the following chart highlights:
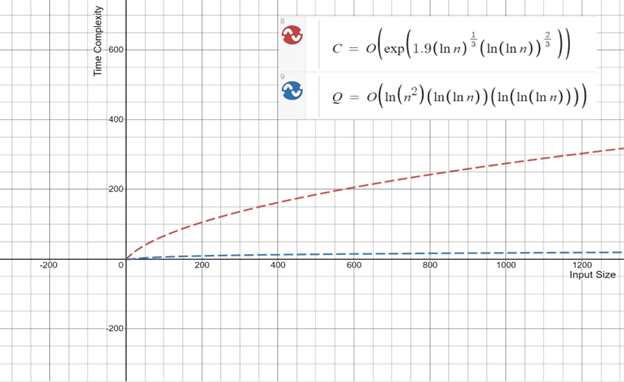
This chart highlights how Quantum computing can execute a problem in a fraction of the time it takes for traditional computing
In the realm of financial markets, this type of computational power could mean analyzing and optimizing vast and diverse investment portfolios in a fraction of the time currently required, allowing for near-real-time adjustments in response to market changes. As such, quantum computing truly represents a new frontier for optimizing investment portfolios, promising unprecedented speed, accuracy, and efficiency.
What is the key advantage of quantum computing?
The prime advantage of quantum computing lies in its sheer speed and efficiency. Through the exploitation of quantum phenomena like superposition and entanglement, quantum computers can process information in ways that are simply beyond the capabilities of classical computers.
Comparing Quantum to Traditional Computing
Let us start our journey of quantum computing by comparing it with traditional computing. The differences become apparent right from the foundational level – the fundamental units of computation.
Qubits instead of Bits
In traditional computing, information is stored in binary ‘bits‘. Each bit is like a tiny switch that can be in one of two positions, represented by 0 or 1. The entire digital world, from the operating system running your computer to the images on your screen, is fundamentally reducible to combinations of these binary bits.
Contrast this with quantum computing, where information is held in ‘qubits‘. A qubit, short for “quantum bit,” is similar to a regular bit with a twist – it can exist not just in a state representing 0 or 1, but also in states representing both 0 and 1 at the same time, thanks to a quantum phenomenon known as superposition. This capability gives quantum computers their multidimensional advantage and is the reason they can process a vast amount of information simultaneously.
Quantum Computer and the Sub-atomic Particles:
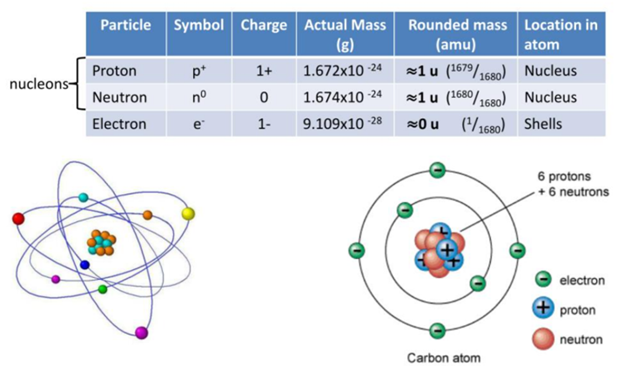
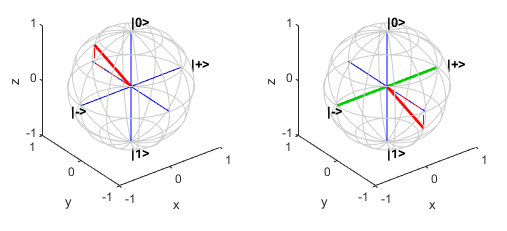
You can visualize the state of single qubit on Bloch sphere in MATLAB:
Visualize State of Single Qubit in Bloch Sphere
To plot any quantum state of a qubit on the Bloch sphere, use the plotBlochSphere function (provided in the Helper Functions section of this doc page). This function takes a complex vector with two elements that represent the probability amplitudes of the ∣0⟩ and ∣1⟩ states.
For example, plot the ∣0⟩ state on the Bloch sphere.

Superposition and entanglement
How do two qubits become entangled? In the derivation below, we can see how two qubits become entangled by sharing the same state no matter how far they are from each other. Once the state of one qubit is measured, the state of the other is settled for certain.
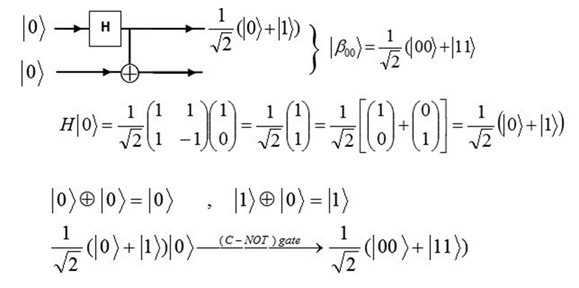
Thus, quantum computing has a different power scaling compared to traditional computing. With traditional computing, an increase in computational power typically follows a linear progression. For each additional bit added to a classical computer, its computational power grows linearly. On the other hand, quantum computers leverage a principle of quantum mechanics called entanglement, which enables a quantum computer to increase its computational power at an exponential rate with each additional qubit.
The applications of these two types of computing could also diverge significantly. Traditional computing is perfect for everyday tasks that require low error rates, such as browsing the internet, word processing, or controlling smart home devices. On the flip side, quantum computing shines when applied to higher-level tasks that require processing vast datasets or running complex simulations. These tasks include but aren’t limited to, running simulations for chemical or drug trials, analyzing large volumes of data for machine learning, and creating energy-efficient batteries.
While traditional computing continues to serve our everyday needs effectively, quantum computing, with its multidimensional, exponential power, is poised to address the complex, large-scale problems that remain beyond the reach of classical machines.
Gate-based quantum computing
Gate-based quantum computing, the method currently viable on existing hardware, revolves around the concept of quantum circuits and algorithms. In this model, qubits are manipulated using a sequence of quantum gates, which are the basic building blocks of quantum circuits. These quantum gates are somewhat analogous to logic gates in classical computing but with a major difference – they can create entanglement and superposition, the fundamental quantum states that give quantum computers their power. Algorithms in gate-based quantum computing represent a set of instructions that dictate the application of these quantum gates to the qubits. Among these algorithms, Shor’s and Grover’s are some of the most famous, offering potential speed-ups for tasks like factorization and search operations.
A Quantum Leap in Portfolio Optimization
Applications in Finance Portfolio Optimization
As we turn our focus toward the impact of quantum computing on finance, it’s particularly interesting to examine its potential role in portfolio optimization. Before delving into how quantum computing can revolutionize this field, let’s take a moment to understand what portfolio optimization entails.
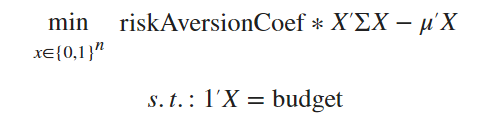
Portfolio optimization is a mathematical framework used in finance to identify the best possible portfolio out of a set of potential investments. The aim is to allocate investments among different financial instruments in a manner that maximizes return and minimizes risk. This involves careful analysis of various parameters such as expected returns, variances, and covariances of asset returns. In essence, portfolio optimization aids investors in making data-driven, strategic investment decisions, thereby maximizing their financial gain while managing potential risks.
Despite its significant role in finance, traditional methods of portfolio optimization face a few major challenges. A prominent hurdle is computational complexity. Classical computers solve optimization problems one step at a time, and as the number of assets in a portfolio grows, the possible combinations and the complexities of the computations increase exponentially. This can result in intractable problems that require prohibitive amounts of computational time and resources.
The second significant challenge is scalability. Classical portfolio optimization methods struggle to scale effectively with increasing portfolio size. As the number of assets increases, classical methods often experience a decline in performance due to the enormous computational resources required to process large datasets. This scalability issue limits the applicability of classical portfolio optimization, particularly for large, complex portfolios.
While traditional methods of portfolio optimization have served us well to date, they are not without their limitations. Computational complexity and limited scalability pose significant challenges, particularly as we handle increasingly large and diverse portfolios. These are precisely the challenges that quantum computing, with its superior speed and ability to handle complexity, promises to overcome. As we will see, the advent of quantum computing in finance may well herald a new era of portfolio optimization.
Benefits of quantum portfolio optimization
With a grasp of the challenges faced by classical methods in portfolio optimization, we can now better appreciate the significant benefits brought about by the incorporation of quantum computing into this field.
The key strength of quantum computing lies in its intrinsic properties of parallelism and interference. Quantum parallelism, derived from the superposition of qubits, allows quantum computers to explore a multitude of potential solutions simultaneously. This is particularly beneficial for portfolio optimization, which often requires a search through a vast space of potential asset combinations. In addition, quantum interference, another fundamental quantum mechanical property, can be harnessed to guide the computational resources toward the most promising solutions, thereby improving the efficiency of the search.
Moreover, a new class of quantum-inspired algorithms, often based on principles like quantum Hamiltonian mechanics, provides fresh approaches to handle complex optimization tasks. These algorithms leverage the principles of quantum mechanics to enhance computational speed and efficiency, even on classical computers.
In the domain of quantum portfolio optimization, several algorithms have already emerged. For instance, the Variational Quantum Eigensolver (VQE) and Quantum Approximate Optimization Algorithm (QAOA) are two notable examples of quantum algorithms applied to financial portfolio optimization. These algorithms exploit the computational power of quantum computers to tackle optimization problems that are intractable for classical computers.
The benefits of quantum portfolio optimization are manifold. The most immediate advantage is speed. Quantum computers, with their ability to process vast amounts of data simultaneously, can dramatically reduce the time taken to optimize portfolios. This, in turn, can lead to more timely investment decisions and strategies.
Furthermore, quantum portfolio optimization offers the potential for greater accuracy. By managing the computational complexities associated with large, diverse portfolios, quantum algorithms can yield solutions that better reflect the true optimal portfolio.
Lastly, the application of quantum computing in portfolio optimization offers unprecedented flexibility. As financial markets become increasingly complex, the ability to adapt and scale with evolving market conditions becomes crucial. Quantum computing, with its exceptional processing power, provides this much-needed flexibility.
Quantum portfolio optimization, empowered by the unparalleled processing capabilities of quantum computing, offers the potential for faster, more accurate, and highly adaptable solutions. This innovative approach holds promise to transform the way we navigate and optimize investment portfolios, ushering in a new era of quantum finance.
What does this look like in MATLAB?
The following example provides a preview of a simulation of the Variational Quantum Eigensolver routine using the Conditional Value at Risk aggregation function. The goal is to show how the problem can be setup and simulated using MATLAB.
Download the example code here
Problem Definition:
Given a set of assets corresponding to expected returns and covariances, along with a risk factor and budget, we seek a subset of assets such that the resulting weighted mean-variance is maximized.
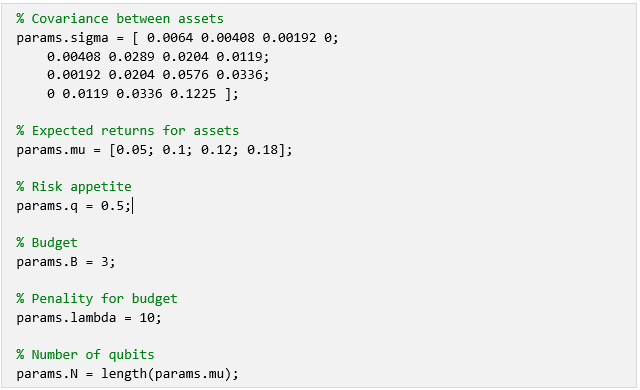
VQE-CVaR Parameters:
To reduce compilation overhead, an ansatz is used that respects the native gate set and connectivity of the Aspen-M-3 device

Simulate the Variational Quantum Eigensolver on a local machine
The objective function for the optimizer takes the angles and simulates an iteration of the VQE-CVaR routine.
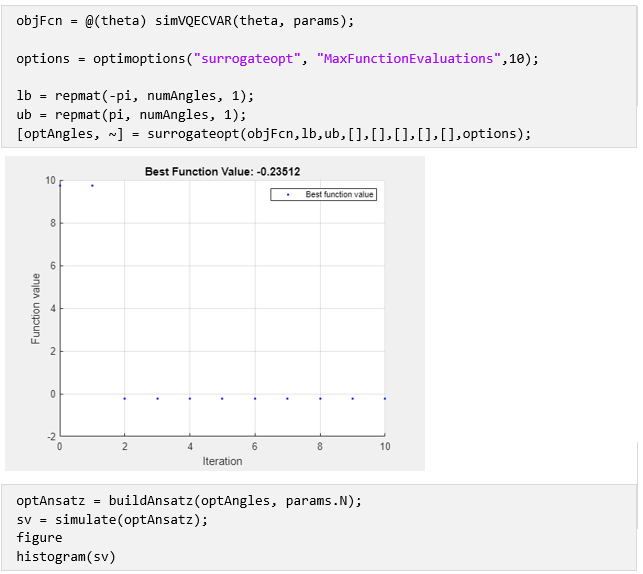
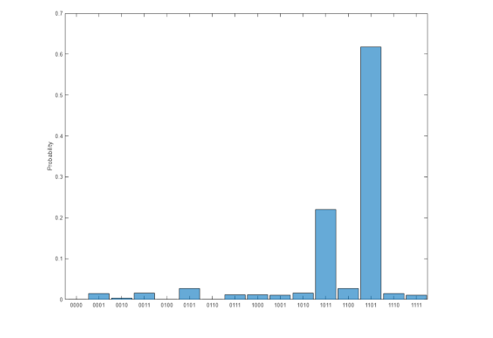
Run the Final Circuit on Quantum Hardware
Run the optimized ansatz circuit on the Aspen-M-3 device provided through Amazon Braket.
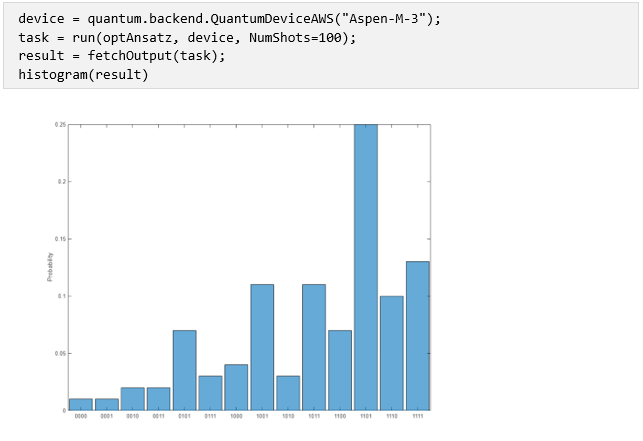
The last 2 plots show, that out of the 14 different portfolio options available, portfolio “1101” returned the highest probability that it was optimal solution.
Deep Dive: Expanding Your Quantum Knowledge
As we delve into the exciting world of quantum computing and its potential applications in finance, it’s always helpful to expand our knowledge base and explore further. Here are some excellent resources that can enhance your understanding of quantum computing.
A fantastic starting point is the article titled “Quantum Computing: Definition, How It’s Used, and Example“on Investopedia. This piece offers a comprehensive overview of quantum computing, its various applications across sectors, and concrete examples to help you grasp the core concepts. This user-friendly guide is a must-read for anyone eager to explore the world of quantum computing.
For those interested in delving into the practical aspects of quantum computing, Mathworks.com provides an extensive resource through the “Quantum Computing with MATLAB” page. This resource offers insightful tutorials and guides that allow you to experiment with quantum algorithms using MATLAB. The Quantum Computing Documentation on MathWorks is another excellent reference, providing an in-depth understanding of how quantum computing works, complete with illustrative examples and useful links.
For readers who want to explore some hands-on applications of quantum computing, I would like to share some examples from my own work and other insightful projects. You can visit this GitHub repository, where I have shared my “PortOpt” project that applies quantum computing principles to portfolio optimization. This will give you a practical example of how quantum algorithms can be implemented to solve real-world problems.
Lastly, the Quantum Support Package is a treasure trove of examples showcasing various quantum computing applications. It’s a brilliant resource if you’re looking to understand the wide-ranging uses of quantum computing across different industries.
In conclusion, while our exploration of quantum computing and portfolio optimization has only scratched the surface, these resources provide an excellent starting point for deeper learning. Quantum computing is a rapidly evolving field, and staying informed and updated is the key to harnessing its potential.








댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.